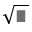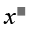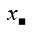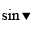Have: n3 - 3n2 + 2 = n3 - n2 - 2n2 + 2

= n2(n - 1) - 2n2 + 2

It is easy to see that n2(n - 1) is an even number because it contains n(n - 1) which is the product of two consecutive natural numbers, so n2(n - 1) - 2n2 + 2 is an even number

But n3 - 3n2 + 2 = n2(n - 1) - 2n2 + 2 is a prime number so n3 - 3n2 + 2 = 2

=> n3 - 3n2 = 0 

<=> n2(n - 3) = 0

According to the topic, n should be positive n = 3

Have: n3 - 3n2 + 2 = n3 - n2 - 2n2 + 2

= n2(n - 1) - 2n2 + 2

It is easy to see that n2(n - 1) is an even number because it contains n(n - 1) which is the product of two consecutive natural numbers, so n2(n - 1) - 2n2 + 2 is an even number

But n3 - 3n2 + 2 = n2(n - 1) - 2n2 + 2 is a prime number so n3 - 3n2 + 2 = 2

=> n3 - 3n2 = 0 

<=> n2(n - 3) = 0

According to the topic, n should be positive n = 

Have: n³ - 3n² + 2 = n³ - n² - 2n² + 2

= n²(n - 1) - 2n² + 2

It is easy to see that n²(n - 1) is an even number because it contains n(n - 1) which is the product of two consecutive natural numbers, so n²(n - 1) - 2n² + 2 is an even number

But n³ - 3n² + 2 = n²(n - 1) - 2n² + 2 is a prime number so n³ - 3n² + 2 = 2

=> n³ - 3n² = 0 

<=> n²(n - 3) = 0

According to the topic, n should be positive n = 3

Let A be the sum,then :

\(-A=\dfrac{-1}{1+\sqrt{2}}+\dfrac{-1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{-1}{\sqrt{98}+\sqrt{99}}+\dfrac{-1}{\sqrt{99}+\sqrt{100}}\)

With \(n\ge0\),we have :

\(\left(\sqrt{n}+\sqrt{n+1}\right)\left(\sqrt{n+1}-\sqrt{n}\right)=\left(n+1\right)-n=1\)

\(\Rightarrow\dfrac{1}{\sqrt{n}+\sqrt{n+1}}=\sqrt{n+1}-\sqrt{n}\)

\(\Rightarrow\dfrac{-1}{\sqrt{n}+\sqrt{n+1}}=\sqrt{n}-\sqrt{n+1}\)

Hence,we have :

\(-A=1-\sqrt{2}+\sqrt{2}-\sqrt{3}+...+\sqrt{98}-\sqrt{99}+\sqrt{99}-\sqrt{100}\)

\(=1-10=-9\)

\(\Rightarrow A=9\)

Because they always lie, then:

- Aron's stone and Bern's stone isn't the same color.

- Bern's stone and Carl's stone isn't the same color.

=> Aron's stone and Carl's stone is the same color.

- Exactly two of them own green stones

=> Aron's stone's and Carl's stone's color is green

=> Bern's stone color is red

So A is the correct answer. (Aron's stone is green)

Since they always lie, we deduce that Aron's stone is the different color from Bern's stone ; Bern's stone is the diferent color from Carl's stone. So, the colors of Aron's and Carl's are the same and different from the color of Bern's. However, exactly 1 of them owns red stones (or exactly two of them own green stones). So, Aron's and Carl's are green ; Bern's is red.

Hence, the answer is (A)

The diameter of the table is: \(\sqrt{20^2+21^2}=\sqrt{400+441}=\sqrt{841}=29\left(ft\right)\)

@8#3@ = (8 + 8) x (6 - 3) = 16 x 3 = 48

What baby wings thin funeral
High bay flying low reported that sunshine rain?
What is the child?

Answer: It's a dragonfly

Oh, yes, welcome to mathyou.com

Post english problems, we will help you
 

thank you so much