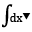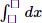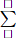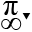Applying the Pythagoras' theorem, we deduce that the length of slant is : \(\sqrt{5^2+\left(1.5\right)^2}=\dfrac{\sqrt{109}}{2}\) (inches)

The area which is covered with chocolate is :

 \(1,5\pi.\dfrac{\sqrt{109}}{2}=\dfrac{3\pi\sqrt{109}}{4}=24.5993926...\approx24.6\)(square inches)

Every time you move, you need to change by 1. To get from 3-9, you must step through 7 different numbers (from 3 to 9). If you deduce 3-2-1-... you won't make to 9.

So there are 7 different numbers.

l do not know english,notvery clear

Consider 4 cases :

+ n = 0 => n⁴ - n + 2 = 2 (unsatisfied)

+ n = 1 => n⁴ - n + 2 = 2 (unsatisfied)

+ n = 2 => n⁴ - n + 2 = 16 = 4² (satisfied)

+ n > 2 

\(\circledast n^4-n+2< n^4\)

\(\circledast\left(n^4-n+2\right)-\left(n^2-1\right)^2=n^4-n+2-n^4+2n^2-1\)

\(=2n^2-n+1=2\left(n^2-\dfrac{1}{2}n+\dfrac{1}{2}\right)\)

\(=2\left(n^2-2n.\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{7}{16}\right)=2\left(n-\dfrac{1}{4}\right)^2+\dfrac{7}{8}>0\)

\(\Rightarrow\left(n^2-1\right)^2< n^4-n+2\)

Hence, n⁴ - n + 2 is between two consecutive perfect squares : (n² - 1)² and (n²)², so n⁴ - n + 2 is not a perfect square

So, n = 2

Phan Thanh Tinh Dao Trong Luan

Let a be the original price of the shirt. We have :

\(\left(1+5\%\right).\left(1-20\%\right)a=15.54\Leftrightarrow105\%.80\%a=15.54\) \(\Leftrightarrow a=18.5\)

So, the answer is $18.50

Because 2017 is a prime number

=> \(F\left(2017\right)=1;2017\)

So their sum is: \(1+2017=2018\)

F=(2017) 1and 2017

the sum is 1+2017=2018

\(n^5-n+2=n\left(n^4-1\right)+2=n\left(n^2+1\right)\left(n^2-1\right)+2\)

\(=n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)+2\)

We see: \(\left(n-1\right)\cdot n\cdot\left(n+1\right)⋮3\) (is product of 3 consecutive natural numbers) 

\(\Rightarrow n^5-n+2\equiv2\left(mod3\right)\)

But no square numbers are in the form 3k + 2

So \(n\notin\varnothing\)

Applying the triangular inequality:
\(12-5< n< 12+5\)
\(\Leftrightarrow7< n< 17\)
So n varies from 8 to 16, therefore there are 9 possible integer values of n

Blue, red, yellow, yellow
The solitary paradise lying alone.
What is the quiz?

Answer: It's a rainbow