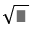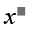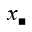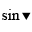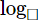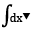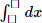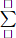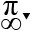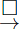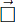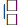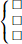Each triangle has an area of : \(\dfrac{s^2\cdot\sqrt{3}}{4}=\dfrac{4^2\cdot\sqrt{3}}{4}=4\sqrt{3}\)(inches).

SUM 4 triangles \(\left(4\sqrt{3}\right)\cdot4=16\sqrt{3}\left(inches\right)\)

The area of the square : \(4^2=16\left(inches\right)\)

The total area is \(16+16\sqrt{3}\left(inches\right)\)

We have \(x^2-2x+1=\left(x-1\right)^2\)

We know that x have 11 values, we apply each values into \(\left(x-1\right)^2\) to calculate, we recognize that only 7 elements that 0,1,4,9,16,25,36 are in set.

The number of remaining cats after the first round is : 66 - 21 = 45

Let x be the number of striped cats with one black ear or the number of finalists. We have the Venn diagram :

Hence : \(27+\left(32-x\right)=45\Leftrightarrow32-x=18\Leftrightarrow x=14\)

So, the answer is D

The number of cats gone to round 2 is: 66 - 21 = 45 (cats)

The minimum number of finalists is: 45 - 32 = 13 (C)

Choose C

\(\dfrac{1}{2}\cdot\dfrac{1}{6}\cdot...\cdot\dfrac{1}{110}=\dfrac{1}{1\cdot2}\cdot\dfrac{1}{2\cdot3}\cdot...\cdot\dfrac{1}{10\cdot11}\)

\(=\dfrac{1}{1\cdot2\cdot2\cdot3\cdot...\cdot10\cdot11}=\dfrac{1}{1\cdot2^2\cdot3^2\cdot...\cdot10^2\cdot11}\)

\(=\dfrac{1}{4\cdot9\cdot16\cdot...\cdot100\cdot11}=\dfrac{1}{13168189440000\cdot11}=\dfrac{1}{144850083840000}\):V, I think the question is:

\(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{110}\)

\(=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{10\cdot11}=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{10}-\dfrac{1}{11}=1-\dfrac{1}{11}=\dfrac{10}{11}\)You should see again and write in English

Call + 1 binder with photos of celebrities on the cover: SB

        + 1 regular binder: RB

We have: \(1SB+8RB=32,60\left(dollars\right)\) and \(1SB+12RB=46,00\left(dollars\right)\)

So we have: \(\left(1SB+12RB\right)-\left(1SB-8RB\right)=4RB=46,00-32,60=13,40\left(dollars\right)\)

So \(1RB=13,40:4=3,35\left(dollars\right)\)

The cost of \(1SB=32,60-\left(3,35\cdot8\right)=5,80\left(dollars\right)\)

So it costs more to buy a celebrity binder than a regular binder: \(5,80-3,35=2,45\left(dollars\right)\)

With x=0 then \(0.f\left(2018\right)=2016.f\left(0\right)\Rightarrow f\left(0\right)=0\)

With x=-2018 then \(-2018.f\left(-2018+2018\right)=\left(-2018+2016\right).f\left(-2018\right)\)

\(\Rightarrow-2018.f\left(0\right)=-2.f\left(-2018\right)\).Because \(f\left(0\right)=0\) so \(-2f\left(-2018\right)=0\Rightarrow f\left(-2018\right)=0\)

So \(f\left(x\right)=0\) with x=0 and -2018

So 

Because x,y are positive integers and \(x\times y=8\)

=> \(\left\{{}\begin{matrix}x=1;y=8\\x=2;y=4\\x=4;y=2\\x=8;y=1\end{matrix}\right.\)

Because \(x^y=y^x\)

=> \(\left\{{}\begin{matrix}x=2;y=4\\x=4;y=2\end{matrix}\right.\)

i think the first x and y are 2 . the second i don't do it

Plowed in the field
Thirsty to drink deep wells black water.
What is the trick?

Answer: it's a pen