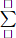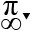P/s : Cho là mình học ngu như longia nói đi những mình tin vào khả năng của mình và mình sẽ không bỏ cuộc 

Còn bạn là người không có đạo đức chưa suy nghĩ trước khi nói

Xin hết !

Nhờ cloud giúp đỡ 

Tao đồng ý với Hương Yêu Dấu nói rất đúng thằng Help you solve math rất ngu

Thằng đấy học ngu lắm

Chắc vậy !

P/s : Bạn không nên đăng những câu hỏi linh tinh như vậy trên diễn đàn:

Tôi mong bạn khắc phục

I don't know?

We can easily prove that P>0.

We have: \(P=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2013^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2012.2013}\)

                                                                 \(=1-\dfrac{1}{2013}< 1\)

\(\Rightarrow0< P< 1\)

So P isn't a integer.

We can easily prove that P>0.

We have: P=122+132+...+120132<11.2+12.3+...+12012.2013

                                                                 =1−12013<1

⇒0<P<1

So P isn't a integer.

In the same year he lived in a house
Parenting in the harmony
The old man was three
An old man was two years old.
What is the trick?

Answer: It's five fingers

We have a sequence of numbers :

\(12;21;30;39;48;B;66;...\)

The numbers separated by 9 units 

=> B = 48 + 9 = 57

So B = 57

hmmmmmmmmmmmmmm......

i dunno

hi im psycho i knifes and i'm 9 years old

B là 57

45 x 6 = 270 (legs )

there are 270 legs of 45 bugs

Maths

                              6 x 45 = 270 ( legs ) 

 MathYou    

The number of legs of 45 bugs are:

6 x 45 = 270 (legs)

            Answer: 270 legs.

Name the points as shown and let a be the length of the side of each small equilateral triangle in cm,then AF = BC = DE = 6 - 2a

The perimeter of the hexagon is : 3a + 3(6 - 2a) = 3(6 - a) = 18 - 3a

The sum of the perimeters of 3 small triangles is : 3a x 3 = 9a

\(\Rightarrow18-3a=9a\Rightarrow12a=18\Rightarrow a=1.5\)

Hence,the answer is D

The answer is B: 1,2cm.

The sum of the perimeters of the 3 small triangles are: \(1,2\cdot3\cdot3=10,8\left(cm\right)\)

The length of the side of the green hexagon is: \(6-1,2\cdot2=3,6\left(cm\right)\)

Because there are 2 sides of the hexagon are not in the perimeter of the big triangle so that the perimeter of the big triangle is: \(10,8\cdot2-\left(10,8:6\cdot2\right)=18\left(cm\right)\) <1>

The perimeter of the big triangle is: \(6\cdot3=18\left(cm\right)\) <2>

Because <1> = <2> \(\left(18cm=18cm\right)\)

=> The side of the small triangle is B: 1,2cm.

The average of 5 days he ate is: \(100:5=20\left(cookies\right)\)

The cookies he eat in 5 days has the distance: \(-12;-6;0;6;12\).

So the cookies he ate on the fifth day is: \(20+12=32\left(cookies\right)\)

Let x be the number of cookies he ate in the 3^rd day,then the number of cookies he ate in the 1^st,2^nd,4^th,5^th are x - 12 ; x - 6 ; x + 6 ; x + 12 \(\left(x>12\right)\) .We have :

\(\left(x-12\right)+\left(x-6\right)+x+\left(x+6\right)+\left(x+12\right)=100\)

\(\Rightarrow5x=100\Rightarrow x=20\Rightarrow x+12=32\)

So,he ate 32 cookies on the fifth day