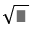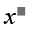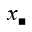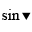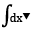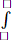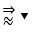Set x + 29 = t       (*)

The given equation becomes: \(\dfrac{1}{t^2}+\dfrac{1}{\left(t+1\right)^2}=\dfrac{5}{4}\)

\(\Leftrightarrow\dfrac{\left(t+1\right)^2+t^2}{t^2\left(t+1\right)^2}=\dfrac{5}{4}\)

\(\Leftrightarrow\dfrac{t^2+2t+1+t^2}{t^2\left(t^2+1+2t\right)}=\dfrac{5}{4}\)

\(\Leftrightarrow4\left(t^2+2t+1+t^2\right)=5t^2\left(t^2+1+2t\right)\)

\(\Leftrightarrow\) 8t² + 8t + 4 = 5t⁴ + 5t² + 10t³

\(\Leftrightarrow\) 5t⁴ + 10t³ - 3t² - 8t - 4 = 0

\(\Leftrightarrow\) 5t⁴ - 5t³ + 15t³ - 15t² + 12t² - 12t + 4t - 4 = 0

\(\Leftrightarrow\left(t-1\right)\left(5t^3+15t^2+12t+4\right)=0\)

\(\Leftrightarrow\left(t-1\right)\left(5t^3+10t^2+5t^2+10t+2t+4\right)=0\)

\(\Leftrightarrow\left(t-1\right)\left(t+2\right)\left(5t^2+5t+2\right)=0\)

\(\Leftrightarrow\left(t-1\right)\left(t+2\right).5.\left[\left(t+\dfrac{5}{4}\right)^2-\dfrac{93}{80}\right]=0\)

\(\Rightarrow\left[{}\begin{matrix}t-1=0\\t+2=0\\\left(t+\dfrac{5}{4}\right)^2-\dfrac{93}{80}=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}t=1\\t=-2\\\left(t+\dfrac{5}{4}\right)^2=\dfrac{93}{80}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}t=1\\t=-2\\t=\dfrac{-25+\sqrt{465}}{20}\\t=\dfrac{-25-\sqrt{465}}{20}\end{matrix}\right.\)

Now just replace (*) is ok

Assume that 0 < a < b < c < d.

The greatest number m formed by using the four digits is \(\overline{dcba}\).

And the least number n formed by using the four digits is \(\overline{abcd}\).

We have: \(\overline{dcba}+\overline{abcd}=1330\)

since \(\overline{abcd}>1000\) and \(\overline{dcba}>1000\) => ​ ​​ ​\(\overline{dcba}+\overline{abcd}>2000\).

Therefore, there is no a, b, c, d sastifies the problem.

The list that 2, 0, 1 and 4 are used to create is :

The sum of all numbers is : 45108.

So the arithmetic mean of all these integers is \(\dfrac{45108}{16}=2506\)

We have : \(x\le1\)\(\Rightarrow\left\{{}\begin{matrix}x^2\le x\\\sqrt{x}\le1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x^2\le x\\x\le\sqrt{x}\end{matrix}\right.\)\(\Rightarrow\sqrt{x}\ge x^2\)

\(\Rightarrow y\sqrt{x}+\dfrac{1}{4}\ge yx^2+\dfrac{1}{4}\) (the equality happens when x = 0 or x = 1)

Moreover, \(yx^2+\dfrac{1}{4}\ge2\sqrt{\dfrac{1}{4}yx^2}=x\sqrt{y}\)

(the equality happens only when \(yx^2=\dfrac{1}{4}\))

So, \(y\sqrt{x}+\dfrac{1}{4}\ge x\sqrt{y}\) or \(x\sqrt{y}-y\sqrt{x}\le\dfrac{1}{4}\)

The equality happens when : \(\left\{{}\begin{matrix}x=1\\yx^2=\dfrac{1}{4}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{1}{4}\end{matrix}\right.\)

B = (x² + 1)(y² + 1) - (x + 4)(x - 4) - (y - 5)(y + 5)

= x²y² + x² + y² + 1 - x² + 16 - y² + 25

= x²y² + 42 \(\ge42\forall x,y\)

The equality happens when :

\(xy=0\Rightarrow\left[{}\begin{matrix}x=0;y\ne0\\x\ne0;y=0\\x=y=0\end{matrix}\right.\)

Tell the commission of Mr. Jones and Mr. Smith  is a and b

a = 3% widgets

b = 5% widgets

=> a/b = 3/5

=> The answer is: 500/5.3 = 300 widgets

mr. jones make commission more than mr. smith:

5-3=2(%)

mr.smith sold

(500:2%)*3=750(widgets)

Mr Smith makes the commission more than Mr Jones: \(5\%-3\%=2\%\)

Mr Smith sold: \(\left(500:2\%\right)\cdot3\%=750\left(widgets\right)\)

No fruit, no tree
But there are seeds falling out of place
The tree fell off happy
Animals find shelter to hide.
What is the quiz?

Answer: It's a raindrops