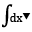-
Dao Trong Luan 21/09/2017 at 09:31\(\dfrac{1}{4\cdot9}+\dfrac{1}{9\cdot14}+...+\dfrac{1}{100\cdot104}\)
\(=\dfrac{1}{5}\left(\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+...+\dfrac{1}{100}-\dfrac{1}{104}\right)\)
\(=\dfrac{1}{5}\left(\dfrac{1}{4}-\dfrac{1}{104}\right)=\dfrac{1}{5}\cdot\dfrac{25}{104}=\dfrac{5}{104}\)
So the value of \(\dfrac{1}{4\cdot9}+\dfrac{1}{9\cdot14}+............+\dfrac{1}{100\cdot104}\)is \(\dfrac{5}{104}\)
Selected by MathYouLike
-
The time now is:
10:30 + 0:55 = 11:25
So the time now to noon is:
12:00 - 11:25 = 0:35
Answer: 35 minutes
Lê Quốc Trần Anh selected this answer.
-
ANSWER:
Danya can get a total of 10 with two or three chips if the first two chips drawn are 4 and 6, which can occur in 2 ways, or if the first three chips drawn are 2, 3 and 5, which can occur in 6 ways. There are 5 × 4 = 20 ways to randomly select two chips, and there are 5 × 4 × 3 = 60 ways to randomly select three chips. The probability that Danya’s total will equal 10 at some point is 2/20 + 6/60 = 1/10 + 1/10 = 2/10 = 0.2
be integers and 
and 
. Find the least possible value for 
of all such triples 
. Prove that your answer is correct.
Lê Quốc Trần Anh Coordinator
23/07/2018 at 02:45
-
Lê Anh Duy 23/07/2018 at 08:27Let b be the number of bunnies (b \(\in\) N* and b < 27)
\(\Rightarrow\) There are 27 - b chicks
\(\Rightarrow\) 4b + 2(27 - b) = 78 (legs)
\(\Leftrightarrow\) 2b = 24
\(\Leftrightarrow\) b = 12
Hence, there are 12 bunnies
P/s: This is the second solution for this math problem. The first one has been worked out by Trịnh
Selected by MathYouLike -
Tôn Thất Khắc Trịnh 23/07/2018 at 07:02The number of chicks is a (creatures) for a\(\in\)N* and a<27
Lê Quốc Trần Anh selected this answer.
The number of bunnies is 27-a (creatures)
We have the equation:
2a+4(27-a)=78
<=>2a+108-4a-78=0
<=>2a=30
<=>a=15(satisfies the condition)
So there are 15 chicks and 27-15=12 bunnies
-
Sherlockkichi 06/08/2018 at 02:31\(D=\left(-2x^3-xy^2\right)+\left(xy^2-1\right)-\left(x^2y-xy^2+3x^2\right)\)
\(D=-2x^3-xy^2+x^2-1-\left(x^2y-xy^2+3x^2\right)\)
\(D=-2x^3-xy^2+xy^2-1-x^2y+xy^2-3x^2\)
\(D=-2x^3-x^2y-3x^2+xy^2-1\)
Selected by MathYouLike
-
Nguyễn Viết Trung Nhân 23/03/2020 at 02:46
The maximum percent error when 24 cm is measured is:
1 : 24 \(\approx\) 4.2%
