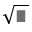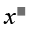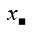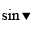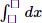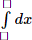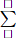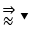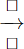-
ANSWER:
There are 8 situations of the cup. Only two of the cups contain three or more dimes. Therefore, the probability that Max randomly selects one of these cups is 2/8 = 1/4.
cannot be expressed in the form 
where 
and 
are rational.-
Alone 06/05/2018 at 17:07Suppose \(\sqrt{2}\) can be expressed in the form \(\dfrac{m}{n}\) with (m,n)=1
\(\Rightarrow\dfrac{m}{n}=\sqrt{2}\Rightarrow\dfrac{m^2}{n^2}=2\)\(\Rightarrow m^2=2n^2\)
Because \(2n^2⋮2\) so \(m^2⋮2\Rightarrow m⋮2\)(1)
\(\Rightarrow m^2⋮4\)\(\Rightarrow n^2⋮2\Rightarrow n⋮2\)(2)
From (1) and (2),we have the assumption is wrong
So \(\sqrt{2}\) can be expressed in the form \(\dfrac{m}{n}\)
Lê Quốc Trần Anh selected this answer.
Lê Quốc Trần Anh Coordinator
23/07/2018 at 02:45
-
Tôn Thất Khắc Trịnh 23/07/2018 at 07:13SILLY has 5 letters
Selected by MathYouLike
S is used once
I is used once
L is used twice
Y is used once
So the number of distinct strings are \(\dfrac{5!}{1!1!2!1!}=60\)
-
\(\dfrac{x}{1.2}+\dfrac{x}{2.3}+\dfrac{x}{3.4}+...+\dfrac{x}{1999.2000}=1\)
\(x\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{1999.2000}\right)=1\)
\(x\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{1999}-\dfrac{1}{2000}\right)=1\)
\(x\left(1-\dfrac{1}{2000}\right)=1\)
\(x.\dfrac{1999}{2000}=1\)
\(x=\dfrac{2000}{1999}\)
Selected by MathYouLike -
FA KAKALOTS 03/02/2018 at 12:41x1.2+x2.3+x3.4+...+x1999.2000=1
x(11.2+12.3+13.4+...+11999.2000)=1
x(1−12+12−13+13−14+...+11999−12000)=1
x(1−12000)=1
x.19992000=1
x=20001999
-
The number of people were selected to be contestants is: \(3000000.\left(1\%.1\%\right)=3000000.\left(0.01\%\right)=300\left(people\right)\)
So the answer is: \(300people\)
