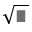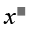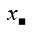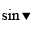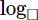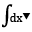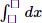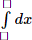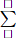-
We have : x*(1*2) = x*(3 - 2) = x*1 = 3x - 1
So 3x - 1 = 2 => 3x = 3 => x = 1
Selected by MathYouLike
-
a) Draw \(AH\perp BD\).
\(\Delta ABE,\Delta ADE\) have the same altitude AH and the bases BE = DE, so \(S_{ABE}=S_{ADE}\) or \(\dfrac{S_{ABE}}{S_{ADE}}=1\)
\(\Rightarrow\dfrac{S_{ABE}}{S_{ABD}}=\dfrac{1}{2}\)
b) Similarly, we have : \(\dfrac{S_{BCE}}{S_{BCD}}=\dfrac{1}{2}\)
\(S_{ABCE}=S_{ABE}+S_{BCE}=\dfrac{1}{2}S_{ABD}+\dfrac{1}{2}S_{BCD}=\dfrac{1}{2}S_{ABCD}\)
Selected by MathYouLike
-
The 3 x 3 x 3 cube which is inside the 5 x 5 x 5 cube comprises the cubes that have no painted face. The answer is : 33 = 27
Lê Quốc Trần Anh selected this answer.
-
Applying the Thales theorem (intercept theorem), we deduce that the coordinates of P are :
\(\left(5\times\dfrac{2}{3};2\times\dfrac{1}{3}\right)=\left(\dfrac{10}{3};\dfrac{2}{3}\right)\)
We have : \(\dfrac{2}{3}=k.\dfrac{10}{3}\Leftrightarrow k=\dfrac{1}{5}\)
-
Nguyen Huu Ai Linh 10/12/2017 at 07:35
Crazy!
-
vuphaminhtien 07/12/2017 at 17:05
wednebe

-
ANSWER:
The probability of pulling out two green socks is 2/5 × 1/4 = 1/10. The probability of pulling out two blue socks is 3/5 × 2/4 = 3/10. The probability, therefore, of randomly pulling out a matching pair of socks is 1/10 + 3/10 = 4/10 = 2/5.