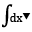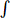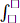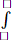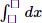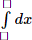So we have 1,2,3,4,6,8,9,12,18,24,36
Then we'll get 1,{1},{1},{1,2},{1,2,3},{1,2,4},{1,3},{1,2,3,4,6},{1,2,3,6,9},{1,2,3,4,6,8,12},{1,2,3,4,6,9,12,18}
Now we'll get 1,{1},{1},{1,[1]},{1,[1],[1]},{1,[1],[1,2]},{1,[1]},{1,[1],[1],[1,2],[1,2,3]},{1,[1],[1],[1,2,3],[1,3]},{1,[1],[1],[1,2],[1,2,3],[1,2,4],[1,2,3,4,6]},{1,[1],[1],[1,2],[1,2,3],[1,3],[1,2,3,4,6],[1,2,3,6,9]}
And then, 1,{1},{1},{1,[1]},{1,[1],[1]},{1,[1],[1,(1)]},{1,[1]},{1,[1],[1],[1,(1)],[1,(1),(1)]},{1,[1],[1],[1,(1),(1)],[1,(1)]},{1,[1],[1],[1,(1)],[1,(1),(1)],[1,(1),(1,2)],[1,(1),(1),(1,2),(1,2,3)]},{1,[1],[1],[1,(1)],[1,(1),(1)],[1,(1)],[1,(1),(1),(1,2),(1,2,3)],[1,(1),(1),(1,2,3),(1,3)]}
Finally, 1,{1},{1},{1,[1]},{1,[1],[1]},{1,[1],[1,(1)]},{1,[1]},{1,[1],[1],[1,(1)],[1,(1),(1)]},{1,[1],[1],[1,(1),(1)],[1,(1)]},{1,[1],[1],[1,(1)],[1,(1),(1)],[1,(1),(1,|1|)],[1,(1),(1),(1,|1|),(1,|1|,|1|)]},{1,[1],[1],[1,(1)],[1,(1),(1)],[1,(1)],[1,(1),(1),(1,|1|),(1,|1|,|1|)],[1,(1),(1),(1,|1|,|1|),(1,|1|)]}

72=2³.3²

To do this, we will calculate the area of the rectangle that has the top left of (a) as the corner, and the bottom right of the cell we are analyzing as the other corner, minus 1
1(a): number 1, so we don't discount anything
2(b): each overlapping 1(a) => 1(one)
2(c): each overlapping 1(a), 1(b) => 1+1=2(ones)
1(d): overlapping 1(a),1(b),1(c) => 1+1+2=4(ones)
1(e): overlapping 1(a),2(b) => 1+2.1=3(ones)
2(f): each overlapping 1(a),2(b),1(c),1(e) => 1+2.1+2+3=8(ones)
1(g): overlapping 1(a),2(b),1(c),1(d),1(e),1(f) => 1+2.1+2+4+3+8=20(ones)
1(h): overlapping 1(a),2(b),2(c),1(e),2(f)=> 1+2.1+2.2+3+2.8=26(ones)
1(i): ignore this guy
So in total, we have 1+2.1+2.2+4+3+2.8+20+26=76(ones)
This took 3 hours for me to figure out... Tell Becky that I hate her sadistic game

\(\dfrac{a-b}{b}=\dfrac{a}{b}-1\).So\(\dfrac{a}{b}-1=\dfrac{3}{5}\Rightarrow\dfrac{a}{b}=\dfrac{8}{5}\)

We have AB + BC + CD + DE = AB + BC' + C'D' + D'E' \(\ge AE'\)

=> min of (AB + BC + CD + DE) = AE' \(=\sqrt{\left(2\right)^2+\left(\dfrac{1}{3}+1+\dfrac{1}{6}\right)^2}=\dfrac{5}{2}\)

When \(B\equiv B'',C'\equiv C'',D'\equiv D''\)

We can infer positions of C, D.

The answer is \(\dfrac{5}{2}\),but I don't know the solution.

Is this problem from USC Mathematics Contest 3/12/1994 ?

Visit here : http://www.math.sc.edu/math-contest-1994-answer-key

Convert: 1 foot = 12 inches, 5 feet 6 inches = 66 inches.

If a human were able to jump, an American will be able to jump: \(66.350=23100\left(inches\right)=1925\left(feet\right)\)

Ta has: abcabc = abc000 + abc 

                      = Abc x 1000 + abc 

                      = Abc. (1000 +1)

                      = Abc. 1001

                      = Abc. 7. 11. 13

The abcabc of the abc with 7; 11; 13 => abcabc divide by 7; 11 and 13

abcabc must to divide : 7 x 11 x 13 = 1001

=> abcabc is : 100100

It's correct

There are 30 rectangles

The number of % of the grapes are not rad are:

100% - 20% = 80%

So the number of the grapes are not red are:

50.80% = 40 [grapes]

So there are 40 grapes are not red

Done ^.^

Số phần trăm nho không đỏ là:

100-20=80%

Số quả nho không đỏ là:

50.80%=40 (quả)

Đáp số: 40 quả

Số phần trăm nho không đỏ là:

100-20=80%

Số quả nho không đỏ là:

50.80%=40 (quả)

Vậy số quả nho không đỏ là 40 quả

We have :

\(\left[{}\begin{matrix}x-2017=0\\x^2-2018^2=0\\x^3-2019^3=0\\x^4-2020^4=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2017\\x=\pm2018\\x=2019\\x=\pm2020\end{matrix}\right.\)

So, the equation has 6 roots above