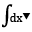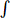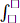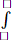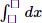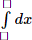We have: 0 \(\times\) (-1) \(\times\) k = 0 - an element in the set

\(\Rightarrow\) With k \(\in\) R, the set {0, -1, k} is always closed under multiplication

Let S = {0, -1, k}.

1. Necessary condition: S is closed under multiplication if  \((-1)\times (-1)\in S\) . It implies \(1\in S\). This means \(k=1\).

2. Sufficient condition: when \(k=1\) , we observe that \(0\times0;0\times-1;-1\times-1;-1\times1;1\times0;1\times1 \)are all in \(S\).
Therefore, \(k=1\).

This is a problem in the newspaper:"Toán học tuổi thơ" that you must be solve it yourself, shouldn't give it to here!!

You can ask your teacher 

i don't understand :((( 

I consider red marble is 3x + 1, yellow marble is 3x + 2, green marble is 3x ( With x \(\in\) N )
Because 2017 = 3x + 1 should :
Color of the 2017^th is red marble.

Since  is on the circle with diameter , we have  and so . We simlarly find that . Also, notice that the line  is the radical axis of the two circles with diameters and . Thus, since  is on , we have  and so by the converse of Power of a Point, the quadrilateral  is cyclic. Thus, . Thus,  and so quadrilateral  is cyclic. Let the circle which contains the points  be cirle . Then, the radical axis of  and the circle with diameter  is line . Also, the radical axis of  and the circle with diameter  is line . Since the pairwise radical axes of 3 circles are concurrent, we have  are concurrent as desired.

Since the product of its digits is 24 > 9,the number must have more than 1 digit.Assume that the number has 2 digits,then we have :

24 = 1 x 24 = 2 x 12 = 3 x 8 = 4 x 6

So,the number can be 38 ; 46 ; 64 ; 83.The smallest of these numbers is 38.The sum of its digits is : 3 + 8 = 11

Hence,the answer is E

Real Egst ?

a) \(x-x^2+x^3-x^4\)

\(\Leftrightarrow x\cdot\left(1-x\right)+x^3\cdot\left(1-x\right)\)

\(\Leftrightarrow\left(x+x^3\right)\cdot\left(1-x\right)\)

b) \(x^2+2x+3x+x\)

\(\Leftrightarrow x\cdot\left(x+6\right)\)

We have : x - x² + x³ - x⁴

= (x - x²) + (x³ - x⁴)

= x(1 - x) + x³(1 - x)

= (1 - x)(x + x³)

= (1 - x).x(1 + x²)

b) ?

The male panda at the local zoo weighs: \(49,35:15\%=49,35:\dfrac{15}{100}=329\left(pounds\right)\)

So the answer is: \(329pounds\)

The weigh of the water in the chemical is : 1000 x 99% = 990 (kg)

Let x kg be the weigh of the evaporated water, then :

\(\dfrac{990-x}{1000-x}=96\%\Leftrightarrow990-x=96\%\left(1000-x\right)\)

\(\Leftrightarrow990-x=960-\dfrac{24}{25}x\Leftrightarrow990-960=-\dfrac{24}{25}x+x\)

\(\Leftrightarrow\dfrac{1}{25}x=30\Leftrightarrow x=750\Leftrightarrow1000-x=250\)

So, the answer is 250 kg

The answer is 250 kg.  100%