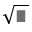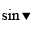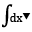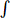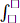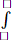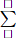-
Vũ Hà Vy Anh 29/05/2017 at 07:212 x2+3x4+4x3 =28
there are 28 wheels in the garage
No Name selected this answer. -
Tina 29/05/2017 at 22:19Have: \(2\cdot2+3\cdot4+4\cdot3=28\left(wheels\right)\)in the garage
-
-
The perimeter of each triangle is : 6 + 10 + 11 = 27
The length of each side of the equilateral triangle is : 27 : 3 = 9
Hence,the answer is D
-
Searching4You 26/07/2017 at 11:18Hiệp Dương : You answer very fast, sir :))
More than 8 lines but you just answer in one minute.
Probably copier :))
-
Hiệp Dương 26/07/2017 at 11:16The number of 4 - digit numbers is:
(9999 - 1000): 1 + 1 = 9000 (number)
If you do not use numbers 2 and 3, then you have eight digits left to form units, tens and hundreds. Since zeros can not be used to make thousands of digits, there are only seven digits left to make thousands.According to the kernel rule, we have:
8 x 8 x 8 x 7 = 3584 (number)
Inference: A 4-digit number containing two digits, or three or both, is 9000 - 3584 = 5416 (number).Answer : 5416 (number).
-
Math You Like 04/09/2017 at 14:56450 + 20 + 50 + 80 + 100
=(450 + 50) + (20 + 80) + 100
=500 + 100 + 100
=700
Kaya Rengest selected this answer. -
Kaya Rengest 04/09/2017 at 15:14
Thank you. You are very good
-
\(\Delta AOD,\Delta COD\) have the same altitude drawn from D to AC and bases \(\dfrac{OA}{OC}=\dfrac{40}{60}=\dfrac{2}{3}\) , so \(\dfrac{S_{AOD}}{S_{COD}}=\dfrac{2}{3}\)
\(\Delta BOC,\Delta COD\) have the same altitude drawn from C to BD and bases \(\dfrac{OB}{OD}=\dfrac{50}{75}=\dfrac{2}{3}\), so \(\dfrac{S_{BOC}}{S_{COD}}=\dfrac{2}{3}\)
\(\Rightarrow S_{AOD}=S_{BOC}\) or the answer is 1
Selected by MathYouLike
-
The whole angles of the square is \(360^0\)
The pizza is cut into 12 congruent slices => Each slice has the angle of \(\dfrac{360}{12}=30^0\)
So the sum of the central angles of the slices that were not eaten after ate 2 slices is :
\(360-30\cdot2=360-60=300^0\)
Answer : \(300^0\)
Selected by MathYouLike
-
\(\widehat{CAB}=180^o-90^o-30^o=60^o\)
\(tan\widehat{CAB}=\dfrac{BC}{CA}\)
\(\Leftrightarrow tan60^o=\dfrac{9}{CA}\Leftrightarrow CA=\dfrac{9}{\sqrt{3}}=3\sqrt{3}\) cm
\(\angle CAD=\dfrac{60^o}{2}=30^o\Leftrightarrow\angle ADC=180^o-90^o-30^o=60^o\)
\(tan\angle ADC=\dfrac{CA}{CD}\)
\(\Leftrightarrow tan60^o=\dfrac{3\sqrt{3}}{CD}\)
\(\Leftrightarrow\sqrt{3}=\dfrac{3\sqrt{3}}{CD}\Leftrightarrow CD=3cm\)
Selected by MathYouLike
grid, Rob starts at 
and needs to reach 
while only moving right or up. Given that he cannot pass through 
, how many distinct paths are possible?
