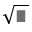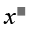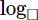There is no reason whatever why Mr. Green's original deposit of $100 should equal the total of the amounts left after each withdrawal. It is just a coincidence that the total of the right-hand column comes as close as it does to $100. This is easily seen by making charts to show a different series of withdrawals. Here are two possibilities: 

As you see, the total on the left must always be $100, but the total on the right can be made very small or very large. Assuming that withdrawals can never involve a fraction of a cent, try to determine the smallest possible total and the largest possible total that the right-hand column can have.

Use Cauchy's inequality for positive numbes a,b,c.

\(a+b\ge2\sqrt{ab},b+c\ge2\sqrt{bc},c+a\ge2\sqrt{ca}\)

\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab}\cdot\sqrt{bc}\cdot\sqrt{ca}=8abc\)

\(\Rightarrow A=\dfrac{abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\le\dfrac{1}{8}\)

\(MaxA=\dfrac{1}{8}\Leftrightarrow a=b=c>0\)

Use Cauchy's inequality for positive numbes a,b,c.

a+b≥2ab−−√,b+c≥2bc−−√,c+a≥2ca−−√

⇒(a+b)(b+c)(c+a)≥8ab−−√⋅bc−−√⋅ca−−√=8abc

⇒A=abc(a+b)(b+c)(c+a)≤18

MaxA=18⇔a=b=c>0

A diference date only appears once/month (Only 1 subtraction is classified). So there will be: 1 difference date/month -> 12 difference date/ year -> 1200 difference date/ century.

So there will be 1200 difference date during the 21st century.

p = 4 + 2² + 2³ + 2⁴ + ... + 2²⁰

=> 2p = 8 + 2³ + 2⁴ +2⁵ +  ... + 2²¹

=> 2p - p = (8 + 2²¹) - (4 + 2²)

=> p = 2²¹

So, p can be written as a power of 2

4 + 22 + 23 + 24 + ... + 220

we have:

22 + 23 + 24 + ... + 220 have 220 - 22 + 1 = 199

And the number of even number are:

\(\left(\text{220 - 20}\right):2+1=102\) [even number]

So the number of odd are:

199 - 102 = 97 [odd]

Because the number of odd is a odd 

=> Their sum are a odd

So 22 + 23 + ... + 220 is a odd

P is a odd

So P can't written as power of 2

Worst case is Peter take out 2 red balls, 2 white balls, 2 yellow balls, all blue ball and black ball.

So Peter taken:

2 + 2 + 2 + 2 + 1 = 9 [balls]

Not three members of the same color, have to take 1 ball more

Number of balls to take are: 9 + 1 = 10 [balls]

Answer 10 balls

But 

But 

We have : The ratio : Charity A : Charity B = 2 : 3.

The money Sam contributes to Charity B is : \(\dfrac{2500}{2+3}\cdot3=1500\)$.

Answer : 1500$.

There are: \(9-1+1=9\left(numbers\right)\) from 100 to 199.

There are: \(9-2+1=8\left(numbers\right)\) from 200 to 299.

................................................................

There are: \(9-9+1=1\left(number\right)\) from 900 to 999.

So there are total is: \(9+8+7+6+5+4+3+2+1=45\left(numbers\right)\)  satisfy the question.

there are:9-1+1=9(numbers)

there are :9-2 +1=8(numbers)

................................................

there are:9-9+1=1(number)

the number of number have 3 digits can disivible by 3 is:

9+8+7+6+5+4+3+2+1=45 (numbers)

answer:45 numbers