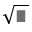We have:

\(8\sqrt{3}=\sqrt{8^2.3}=\sqrt{64.3}=\sqrt{192}\)

\(5\sqrt{7}=\sqrt{5^2.7}=\sqrt{25.7}=\sqrt{175}\)

Because 192>175 so \(\sqrt{192}>\sqrt{175}\)

or \(8\sqrt{3}>5\sqrt{7}\) 

#35# = 35 x 1 x 2 x 3 = 35 x 6 = 210

Answer: No one is lying because the 3 of them are 3 sisters of Thien

After transferred, each box has:

      48 : 3 = 16(apples)

The original number of apples in container A  is:

      16 + 9 = 25( apples)

Assume x be the correct seuqence in {a, b, c, d, e}, we infer the distance between x and the other sequences would be in a set of {1, 2, 3, 4}. (the distance here is the number of different positions in the two sequences)

We have:

+ With sequence a: distance(a,b) = 2, distance(a,c) = 3, distance(a,d) = 3, distance(a,e) = 2.

  => a is not correct sequence because {2, 3, 3, 2} differs {1, 2, 3, 4}

+ With sequence b: distance(b,a) = 2, distance(b,c) = 1, distance(b,d) = 3, distance(b,e) = 4.

  => b should be the correct sequence because {2, 1, 3, 4} = {1, 2, 3, 4}.

+ With sequence c: distance(c,a) = 3, distance(c,b) = 1, distance(c,d) = 4, distance(c,e) = 5.

  => c is not correct sequence because {2, 1, 4, 5} differs {1, 2, 3, 4}

+ With sequence d: distance(d,a) = 3, distance(d,b) = 3, distance(d,c) = 4, distance(d,e) = 1.

  => d is not correct sequence because {3, 3, 4, 1} differs {1, 2, 3, 4}

+ With sequence e: distance(e,a) = 2, distance(e,b) = 4, distance(e,c) = 5, distance(e,d) = 1.

  => d is not correct sequence because {2, 4, 5, 1} differs {1, 2, 3, 4}.

So the correct sequence is b.

We have: \(\dfrac{x}{\sqrt{91^2-x^2}}=\dfrac{60-x}{60}\)

We find \(x=35\)

This is the short solution :

.........................

BI is the bisector,so I is equidistant from BA and BC or IM = IP

AI is the bisector,so I is equidistant from AB and AC or IM = IN

\(\Rightarrow IN=IP\) => I is equidistant from CA and CB

=> CI is the bisector ray of \(\widehat{C}\)

Hence, ..................................

Given \(\Delta ABC\).Let I be the intersection of the bisectors of \(\widehat{BAC}\) and \(\widehat{ABC}\).Draw \(IM\perp AB;IN\perp AC;IP\perp BC\)

\(\Delta IMA\) right at M and \(\Delta INA\) right at N have the common side IA ; \(\widehat{A_1}=\widehat{A_2}\) (since AI is the bisector)

\(\Rightarrow\Delta IMA=\Delta INA\) (hypotenuse - acute angle)

\(\Rightarrow IM=IN\) (2 corresponding sides)

\(\Delta IMB\)  right at M and \(\Delta IPB\) right at P have the common side IB ; \(\widehat{B_1}=\widehat{B_2}\) (since BI is the bisector)

\(\Rightarrow\Delta IMB=\Delta IPB\) (hypotenuse - acute angle)

\(\Rightarrow IM=IP\) (2 corresponding sides)\(\Rightarrow IN=IP\)

\(\Delta INC\) right at N and \(\Delta IPC\) right at P have the common side IC ; IN = IP,so \(\Delta INC=\Delta IPC\) (hypotenuse - leg)

\(\Rightarrow\widehat{C_1}=\widehat{C_2}\) (2 corresponding angles) => CI is the bisector of \(\widehat{ACB}\)

Hence, three bisectors of \(\Delta ABC\) are convergent at I

We have :

M = 2(a³ + b³) - 3(a² + b²)

M = 2.(a + b).(a² - ab + b²) - 3.[(a + b)² - 2ab]

M = 2(a² - ab + b²) - 3.1 + 3.2ab

M = 2a² - 2ab + 2b² - 3 + 6ab

M = 2a² + 4ab + 2b² - 3

M = 2.(a² + 2ab + b²) - 3

M = 2.(a + b)² - 3

M = 2 - 3 = -1 

We have :

M = 2(a3 + b3) - 3(a2 + b2)

M = 2.(a + b).(a2 - ab + b2) - 3.[(a + b)2 - 2ab]

M = 2(a2 - ab + b2) - 3.1 + 3.2ab

M = 2a2 - 2ab + 2b2 - 3 + 6ab

M = 2a2 + 4ab + 2b2 - 3

M = 2.(a2 + 2ab + b2) - 3

M = 2.(a + b)2 - 3

M = 2 - 3 = -1

Let A be the number of bricks needed to build a structure 12 levels high

We have :

\(A=1.2+2.3+3.4+...+11.12+12.13\)

\(3A=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+11.12.\left(13-10\right)+12.13.\left(14-11\right)\)

\(=\left(1.2.3+2.3.4+3.4.5+...+11.12.13+12.13.14\right)-\left(1.2.3+2.3.4+..+10.11.12+11.12.13\right)\)

\(=12.13.14=3.4.13.14\)

\(A=4.13.14=728\)

So,the answer is 728 bricks