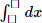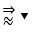Suppose that it takes Alice x hours to go from A to B. Then, it takes Bill x + 2.5 hours to go from B to A. We get that Alice’s speed is d/x and Bill’s speed is d/(x + 2.5), where d is the distance from A to B. Since Alice and Bill met 3 hours after they started walking, we have:

  \(3\left(\dfrac{d}{x}+\dfrac{d}{x+2,5}\right)=d\)

\(\Rightarrow x=5\).

So Bill take 5 + 2,5 = 7,5 hours to go from B to A.

The amount must have been $31.63. He received $63.31. After he had spent a nickel there would remain the sum of $63.26, which is twice the amount of the check. 

There are 2 vertices in the left triangle that can connect to 2 vertices in the right triangle. So there are \(2.2=4\left(ways\right)\)

ANSWER: 4 ways.

There are 2 ways as shown :

From \(a^3+b^3+c^3=3abc\Rightarrow a^3+b^3+c^3-3abc=0\)

\(\Rightarrow a^3+3ab(a+b)+b^3+c^3-3abc-3ab(a+b)=0\)

\(\Rightarrow (a+b)^3+c^3-3ab(a+b+c)=0\)

\(\Rightarrow (a+b+c)(a^2+2ab+b^2-ab-ac+c^2)-3ab(a+b+c)=0\)

\(\Rightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ca)=0\)

It's right because \(a+b+c=0\)

We have :

a³ + b³ + c³ = 3abc 

a³ + b³ + c³ - 3abc = 0

(a³ + 3a²b + 3ab² + b³) + c³ - 3a²b - 3ab² - 3abc = 0

(a + b)³ + c³ - 3ab.(a + b + c) = 0

[(a + b) + c].[(a + b)² - c.(a + b) + c²] - 3ab(a + b + c) = 0

(a + b + c).[a² + 2ab + b² - ac - bc + c²] - 3ab(a + b + c) = 0

(a + b + c).[a² + b² + c² - bc - ca + 2ab - 3ab] = 0

(a + b + c).[a² + b² + c² - ab - bc - ca] = 0

That is right , because a + b + c = 0

So a³ + b³ + c³ = 3abc

With a + b + c = 0

If \(a,b,c\in N\) then I can answer it.

\(a+b+c=0\)

=> \(a=b=c=0\).

Because \(\forall x\) in the case \(0^x=0\) and a number multiplies by \(0\) equals to \(0\).

=> \(a^3+b^3+c^3=3abc=0\left(proved\right)\)

- There are \(\dfrac{363-3}{10}+1=37\) digit 3 do units

- There are \(\dfrac{330-30}{100}+1=4\) digit 3 do tenth

- There are \(\dfrac{399-300}{1}+1=100\) digit do hundredth

So there are 100 + 4 + 37 = 141 digit 3 appear as part of a page number of this book

Let x, y be the numbers (x > y). We have :

\(\left\{{}\begin{matrix}x-y=6\\x^2-y^2=24\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x-y=6\\\left(x-y\right)\left(x+y\right)=24\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x-y=6\\x+y=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=y+6\\2y=-2\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\)\(\Rightarrow xy=-5\)

So, the answer is -5

Call the bigger numbers a, the smaller number b

We have: a-b=6 and a+b=24

=> a-b+a+b=6+24

=>2a=30

=>a=30:2

=>a=15

=> 15-b=6

=>b=9

So the products of the two numbers are 15 and 9

B = \(\dfrac{0,00000025.0,00006}{0,0000000015}\) = \(\dfrac{25.10^{-8}.6.10^{-5}}{15.10^{-10}}\) = \(\dfrac{6.25.10^{-13}}{15.10^{-10}}\) = \(\dfrac{150}{15}.10^{-3}=10.10^{-3}=10^{-2}\)

    => B = \(\dfrac{1}{10^2}\) = 0,01

B = 0,00000025.0,000060,0000000015 = 25.10−8.6.10−515.10−10 = 6.25.10−1315.10−10 = 15015.10−3=10.10−3=10−2

    => B = 1102

 = 0,01

i think the title is wrong. It is: 34(AB+AC+BC)<AD+BE+CF<AB+AC+BC

I think the title is wrong. It is: \(\dfrac{3}{4}\left(AB+AC+BC\right)< AD+BE+CF< AB+AC+BC\)