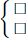42 = 2 x 3 x 7

85! = 1 . 2 . 3 ... 85

85! has 12 factors \(⋮7\), including: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84.

Among these factors, 47 = 7 . 7. So 85! has 13 factors \(⋮\) 7. So k = 13

85!=1 x 2 x 3 x ... x 84 x 85

42=2 x 3 x7

85! has 42 numbers \(⋮\)2

______28 _______ \(⋮\)3

______12________\(⋮\)7

=> k=12.

The illustration shows the supremely easy way of solving this puzzle. The central star is the officer, and the dots are the men. 

Draw the altitudes as shown

\(\Delta ABD,\Delta ADC\) have the common altitude AH and the bases BD = DC,so \(S_{\Delta ABD}=S_{\Delta ADC}\)

\(\Delta IBD,\Delta IDC\) have the common altitude IK and the bases BD = DC,so \(S_{\Delta IBD}=S_{\Delta IDC}\)

\(\Rightarrow S_{\Delta ABD}-S_{\Delta IBD}=S_{\Delta ADC}-S_{\Delta IDC}\Rightarrow S_{\Delta AIB}=S_{\Delta AIC}\)

\(\Delta AIE,\Delta AIC\) have the common altitude IN and the bases \(AE=\dfrac{1}{3}AC\),so \(S_{\Delta AIE}=\dfrac{1}{3}S_{\Delta AIC}=\dfrac{1}{3}S_{\Delta AIB}\)

\(\Rightarrow\dfrac{S_{\Delta AIE}}{1}=\dfrac{S_{\Delta AIB}}{3}=\dfrac{S_{\Delta AIE}+S_{\Delta AIB}}{1+3}=\dfrac{S_{\Delta ABE}}{4}\)

\(\Rightarrow\dfrac{S_{\Delta AIE}}{S_{\Delta ABE}}=\dfrac{1}{4}\)

\(\Delta ABE,\Delta ABC\) have the common altitude BM and the bases \(AE=\dfrac{1}{3}AC\),so \(\dfrac{S_{\Delta ABE}}{S_{\Delta ABC}}=\dfrac{1}{3}\)

\(\Rightarrow\dfrac{S_{\Delta AIE}}{S_{\Delta ABE}}\times\dfrac{S_{\Delta ABE}}{S_{\Delta ABC}}=\dfrac{1}{4}\times\dfrac{1}{3}\Rightarrow\dfrac{S_{\Delta AIE}}{S_{\Delta ABC}}=\dfrac{1}{12}\)

surf before ask Câu hỏi của Mai Nguyễn Bảo Ngọc - Toán lớp 8 | Học trực tuyến

A = (x² + y²)³ + (z² - x²)³ - (y² + z²)³

A = [(x² + y²) + (z² - x)²]³ + 3.(x² + y²).(z² - x²).(x² + y² + z² - x²) - (y² + z²)³

A = (y² + z²)³ + 3.(x² + y²).(x + z)(z - x).(y² + z²) - (y² + z²)³

A = 3.(x² + y²).(x + z)(z - x).(y² + z²) 

Kayasari Ryuunosuke:Congratulation!! You're wrong

Since 5! = 1.2.3.4.5 = 10.3.4, 5! ends by 0 and 6!, 7!, 8!,..., 2014! both end by 0. We have :

\(1!+2!+3!+...+2014!\equiv1+2+6+24+0\)

\(\equiv33\equiv3\) (mod 10)

So, the answer is 3
 

Nối A,B,C. Suy ra AC=12cm

Gọi N là tiếp điểm 2 đường tròn suy ra AN=6cm

Sử dụng Pytagor

Suy ra Bán kính r của đường tròn nhỏ là 2cm

Cut in half so 72/2=36 is the diameters of two circles.

Sum of the areas : \(2S=\dfrac{d^2}{4}\cdot3,14\cdot2=2034,72\left(cm^2\right)\)

Answer : 2034,72 \(cm^2\).

From the question, we deduce that the third term is 36. The remaining terms are : 

\(36:\left(1.5\right)^2=16\)

\(36:1.5=24\)

\(36\times1.5=54\)

\(36\times\left(1.5\right)^2=81\)

The answer is : \(\dfrac{16+24+36+54+81}{5}=42.2\)

\(\left\{{}\begin{matrix}a\le a^2\\b\le b^2\\c\le c^2\end{matrix}\right.\Rightarrow a^2+b^2+c^2\ge a+b+c\ge abc\)

So \(a^2+b^2+c^2\ge abc\)