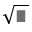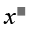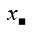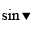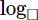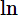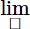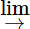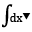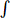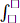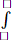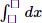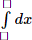-
→இے๖ۣۜBoy™†hïếuGîa 31/05/2017 at 16:44
a) 46;64
b) We have:
3=0+1+23=0+1+26=1+2+36=1+2+3
11=2+3+611=2+3+6
⇒6+11+20=37
-
NVH_HVN 30/05/2017 at 21:57
a) 46;64
b) We have:
3=0+1+23=0+1+26=1+2+36=1+2+3
11=2+3+611=2+3+6
⇒6+11+20=37
-
-
Let D be the number of quarters, then D - 6 and D - 4 are the numbers of nickels and dimes respectively \(\left(D\in N;D-6>0\Leftrightarrow D>6\right)\)
Convert : 1 nickel = 5 cents ; 1 dime = 10 cents ; 1 quarter = 25 cents
$5.30 = 530 cents
We have :
\(5\left(D-6\right)+10\left(D-4\right)+25D=530\)
\(\Leftrightarrow5D-30+10D-40+25D=530\)
\(\Leftrightarrow40D=600\Leftrightarrow D=15\)
So,this collection of coins has 15 quarters
-
The biggest and the smallest 3-digit number each formed by different digits is 987 and 102. Their difference is : 987 - 102 = 885
-
VTK-VangTrangKhuyet 04/09/2017 at 21:25
1 human fingernail : 3mm/1month
10 human fingernails : 30mm/1month
=> 10 human fingernails : 360mm/1 year.
=> 10 human fingernails : 3600mm/10 years.
So the total meters of Deshawn’s 10 fingernails will grow over the next 10 years is 3600mm=3,6m.
Answer : 3,6 meters.
Selected by MathYouLike
-
The sum of the factors of 120 which are different from 3 and 8 is :
4 + 5 + 6 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 346
So, the answer is 346