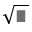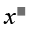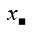(x + 2) : 2 = (5x - 8) : 4

=> \(\dfrac{x+2}{2}=\dfrac{5x-8}{4}\)

<=> 4(x + 2) = 2(5x - 8)

<=> 4x + 8 = 10x - 16

=> 24 = 6x

=> x = 4

(x + 2) : 2 = (5x - 8) : 4

=> x+22=5x−84

<=> 4(x + 2) = 2(5x - 8)

<=> 4x + 8 = 10x - 16

=> 24 = 6x

=> x = 4

Mai has notebooks is :

     3+4=7 notebooks

James has notebooks is :

      7+4=11 notebooks

           Answer : 11 notebooks

Mai has notebooks is :

     3+4=7 notebooks

James has notebooks is :

      7+4=11 notebooks

           Answer : 11 notebooks

Mai's notebooks: \(4+3=7\left(notebooks\right)\)

James's notebooks: \(4+7=11\left(notebooks\right)\)

Answer: James has 11 notebooks

Name the points as shown

We have : OA = OB = OC = OD = 5 cm

Draw the altitude OH of \(\Delta OCD\),then it's also a median

\(\Rightarrow DH=\dfrac{CD}{2}=\dfrac{8}{2}=4\) (cm)

Applying the Pythagoras theorem to the right \(\Delta OHD\),we have :

\(OH=\sqrt{OD^2-DH^2}=\sqrt{5^2-4^2}=\sqrt{9}=3\) (cm)

\(\Delta ADC,\Delta ODC\) have the common altitude DI and the bases AC = 2OC, so \(S_{ADC}=2S_{ODC}\)

\(S_{ABCD}=CD.AD=2.\dfrac{CD.AD}{2}=2.S_{ADC}=2.2.S_{ODC}\)

\(=4.\dfrac{OH.CD}{2}=2.3.8=48\) (cm²)

48 cm

đúng 1000000000000%

50 + 300 + 50 + 100

= ( 50 + 50 ) + ( 300 + 100 )

= 100 + 400

= 500

   50+300+50+100

=(50+50)+(300+100)

=100+400

=500

50 + 300 + 50 + 100

= ( 50 + 50 ) + ( 300 + 100 )

= 100 + 400

= 500

We have: abc + bb = cba.

=> b = 9, a > 5 and c - a = 1 (the only situation satisfy)

So the numbers abc are: 596;697;798

P/s: with \(a\ne b\ne c\) and no proving.

The perimeter of the hexagon is:

6.6 = 36 [cm]

So perimeter of this hexagon is 36cm

 The perimeter of the hexagon is:

6.6=36 (cm)

 The perimeter of this hexagon is: 36cm

The perimeter of the hexagon is:

6.6=36 (cm)

So the result is: 36 (cm)

Because x+y creates 1 part 2 of a diagonal line of the square so \(x+y=\sqrt{\dfrac{4}{2}}=\sqrt{2}\)

So x+y=\(\sqrt{z}\Rightarrow\sqrt{2}=\sqrt{z}\Rightarrow z=2\)

Answer:The value of z is:2

Chúng ta có: x + y =\(\sqrt{\dfrac{4}{2}}=\sqrt{2}\) because x+y creates 1 part 2 of a diagonal line

So x+y=\(\sqrt{z}\Rightarrow\sqrt{2}=\sqrt{z}\)\(\Rightarrow z=2\)

Answer:z=2

ANSWER:

Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, … . It appears that every fifth multiple of 3 is also a multiple of 5. The percent probability that a randomly selected multiple of 3 is also a multiple of 5 is 1/5 = 20%.