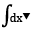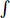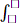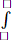\(5\cdot\left(11+4:4\right)\)

\(=5\cdot\left(11+1\right)\)

\(=5\cdot12=60\)

The volume of the cup is : \(\left(\dfrac{6}{2}\right)^2\pi.12=108\pi\) (cm³)

The volume of 48 tapioca bubbles is : \(108\pi-100\pi=8\pi\) (cm³)

The volume of each tapioca bubble is : \(\dfrac{8\pi}{48}=\dfrac{\pi}{6}\) (cm³)

The answer is : \(\sqrt[3]{\dfrac{\pi}{6}:\dfrac{4\pi}{3}}=0.5\) (cm)

Tell the praction to find is \(\dfrac{a}{b}\)

\(\Rightarrow\left\{{}\begin{matrix}b-a=8\\\dfrac{2a}{b-1}=1\end{matrix}\right.\)

=> a + a = b - 1

=> a + 1 = b - a  = 8

=> a = 7

=> b = 15

So the fraction to find is \(\dfrac{7}{15}\)

Tell the praction to find is ab

⇒⎧⎨⎩b−a=82ab−1=1

=> a + a = b - 1

=> a + 1 = b - a  = 8

=> a = 7

=> b = 15

So the fraction to find is 715

Tell the praction to find is 

=> a + a = b - 1

=> a + 1 = b - a  = 8

=> a = 7

=> b = 15

So the fraction to find is 

We have :

X * 45 + X * 34 + X * 45

= X * ( 45 + 34 + 45 )

= X * 134

So X can not be worth being 

P/s : Invalid, wrong

Hey how much is it equal to?

Each day, all three plant produce the number of cars is:

100 + 80 + 70 = 250 (cars)

So, need the number of full days to produce 1600 cars is :

1600 : 250 = 6,2 days 

So need 7 full days to produce 1600 cars

Since no box are labeled correct; box 3 must have baseballs only.So easy that box 2 contains only tennis balls.

Let I be the center of the circle is inscribed in right triangle ABC.
Because CI, AI, BI is bisector of \(\widehat{C};\widehat{A};\widehat{B}\) , we have:
\(\widehat{FAI}=\widehat{DAI};\widehat{DBI}=\widehat{EBI};\widehat{FCI}=\widehat{ECI}.\)
So: \(\Delta AFI=\Delta ADI;\Delta BEI=\Delta BDI;\Delta CIF=\Delta CIE\).
Deduced: \(AF=AD=7;DE=BD=13;CE=CF\).
\(AB=AD+DB=3+13=20\).
Apply theorem Pi-ta-go in \(\Delta CAB\) , we have:
\(AC^2+BC^2=AB^2\) \(\Leftrightarrow\left(AF+CF\right)^2+\left(CE+BE\right)^2=AB^2\)
                                    \(\Leftrightarrow\left(7+CF\right)^2+\left(13+CE\right)^2=20^2\)
                                    \(\Leftrightarrow\left(7+CE\right)^2+\left(13+CE\right)^2=20^2\) (because CE = CF )
                                    \(\Leftrightarrow2CE^2+40CE-182=0\)

                                    \(\Leftrightarrow CE=-10+\sqrt{191}\)
\(AC=7-10+\sqrt{191}=-3+\sqrt{191}\); \(BC=13-10+\sqrt{191}=3+\sqrt{191}\).
\(S_{\Delta ACB}=\dfrac{AC\times BC}{2}=\dfrac{\left(-3+\sqrt{191}\right)\left(3+\sqrt{191}\right)}{2}=91\).