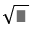\(A=1\cdot3\cdot5\cdot...\cdot99\)

\(\Rightarrow2\cdot4\cdot6\cdot...\cdot100\cdot A=1\cdot2\cdot3\cdot4\cdot...\cdot100\)

\(\Rightarrow A=\dfrac{1\cdot2\cdot3\cdot...\cdot100}{2\cdot4\cdot6\cdot...\cdot100}=\dfrac{\left(1\cdot2\cdot3\cdot4\cdot...\cdot50\right)\cdot\left(51\cdot52\cdot...\cdot100\right)}{\left(2\cdot1\right)\left(2\cdot2\right)\left(2\cdot3\right)...\left(2\cdot50\right)}\)\(A=\dfrac{\left(1\cdot2\cdot3\cdot...\cdot50\right)\left(51\cdot52\cdot...\cdot100\right)}{2^{50}\cdot\left(1\cdot2\cdot3\cdot...\cdot50\right)}=\dfrac{51\cdot52\cdot...\cdot100}{2^{50}}=\dfrac{51}{2}\cdot\dfrac{52}{2}\cdot...\cdot\dfrac{100}{2}=B\)So A = B

If a=12,b=4,c=5 and x=\(\dfrac{1}{2}\) so \(\dfrac{\left(\dfrac{abc}{x}\right)-\left(6b^2-4\right)}{0,5}\)\(=\dfrac{\left(\dfrac{12.4.5}{\dfrac{1}{2}}\right)-\left(6.4^2-4\right)}{0,5}\)

\(=\dfrac{\left(\dfrac{240}{\dfrac{1}{2}}\right)-\left(96-4\right)}{0,5}=\dfrac{480-92}{0,5}=\dfrac{388}{\dfrac{1}{2}}=388.2=776\)

Answer:776`

Condition : \(x\ne3;-5\)

\(\dfrac{x+5}{3}-\dfrac{x-3}{5}=\dfrac{5}{x-3}-\dfrac{3}{x+5}\)

\(\Leftrightarrow\dfrac{5\left(x+5\right)-3\left(x-3\right)}{15}=\dfrac{5\left(x+5\right)-3\left(x-3\right)}{\left(x-3\right)\left(x+5\right)}\)

\(\Leftrightarrow\left(2x+34\right)\left(\dfrac{1}{15}-\dfrac{1}{\left(x-3\right)\left(x+5\right)}\right)=0\)

\(\Leftrightarrow\left(x+17\right).\dfrac{\left(x-3\right)\left(x+5\right)-15}{15\left(x-3\right)\left(x+5\right)}=0\)

\(\Leftrightarrow\left(x+17\right)\left(x^2+2x-30\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x+17=0\\x^2+2x-30=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=-17\\x=-1\pm\sqrt{31}\end{matrix}\right.\)(satisfied)

So, \(S=\left\{-17;-1\pm\sqrt{31}\right\}\)

Condition : x≠3;−5

x+53−x−35=5x−3−3x+5

⇔5(x+5)−3(x−3)15=5(x+5)−3(x−3)(x−3)(x+5)

⇔(2x+34)(115−1(x−3)(x+5))=0

⇔(x+17).(x−3)(x+5)−1515(x−3)(x+5)=0

⇔(x+17)(x2+2x−30)=0

⇒[x+17=0x2+2x−30=0

⇒[x=−17x=−1±√31

(satisfied)

So, S={−17;−1±√31}

Because  \(\dfrac{12x}{25}\) is a square number but 12=2².3

So \(x⋮25\) and x smallest so x=3.25=75

I solved the first way for you.This is the second way :

We have :\(x^2-5x+4=0\Rightarrow a=1;b=-5;c=4\)

\(\Rightarrow b^2-4ac=25-16=9>0\)\(\Rightarrow\sqrt{b^2-4ac}=3\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5+3}{2}=4\\x=\dfrac{5-3}{2}=1\end{matrix}\right.\)

Summer Clouds

 I solved the first way for you.This is the second way :

We have :$x^2-5x+4=0\Rightarrow a=1;b=-5;c=4$${\mathrm{<i>x</i>}}^{\mathrm{<i>2</i>}}<i>-</i>\mathrm{<i>5</i>}\mathrm{<i>x</i>}<i>+</i>\mathrm{<i>4</i>}<i>=</i>\mathrm{<i>0</i>}<i>\Rightarrow </i>\mathrm{<i>a</i>}<i>=</i>\mathrm{<i>1</i>}<i>;</i>\mathrm{<i>b</i>}<i>=</i><i>-</i>\mathrm{<i>5</i>}<i>;</i>\mathrm{<i>c</i>}<i>=</i>\mathrm{<i>4</i>}$

$\Rightarrow b^2-4ac=25-16=9>0$$<i>\Rightarrow </i>{\mathrm{<i>b</i>}}^{\mathrm{<i>2</i>}}<i>-</i>\mathrm{<i>4</i>}\mathrm{<i>a</i>}\mathrm{<i>c</i>}<i>=</i>\mathrm{<i>25</i>}<i>-</i>\mathrm{<i>16</i>}<i>=</i>\mathrm{<i>9</i>}<i>></i>\mathrm{<i>0</i>}$$\Rightarrow \sqrt{b^2-4ac}=3$$<i>\Rightarrow </i>\sqrt{{\mathrm{<i>b</i>}}^{\mathrm{<i>2</i>}}<i>-</i>\mathrm{<i>4</i>}\mathrm{<i>a</i>}\mathrm{<i>c</i>}}<i>=</i>\mathrm{<i>3</i>}$

$\Rightarrow [\begin{array}{c}x=\frac{5+3}{2}=4\end{array}$$\begin{array}{c}x=\frac{5-3}{2}=1\end{array}$

\(2^{51}-1=2^{3.17}-1=8^{17}-1=\left(8-1\right).\left[\left(8^{17-1}\right)+\left(8^{17-2}\right)+...+\left(8^{17-16}\right)+8^{17-17}\right]\) is divisible by 7.

Let n be the number of sides of the regular polygon\(\left(n\in N;n\ge3\right)\),then the measure of each interior angle is \(\dfrac{180\left(n-2\right)}{n}\) and the measure of each exterior angle is \(180-\dfrac{180\left(n-2\right)}{n}\).We have :

\(\dfrac{180\left(n-2\right)}{n}=8\left(180-\dfrac{180\left(n-2\right)}{n}\right)\)

\(\Leftrightarrow\dfrac{180\left(n-2\right)}{n}-1440+8.\dfrac{180\left(n-2\right)}{n}=0\)

\(\Leftrightarrow9.\dfrac{180\left(n-2\right)}{n}=1440\Leftrightarrow\dfrac{9\left(n-2\right)}{n}=8\Rightarrow9n-18=8n\Leftrightarrow n=18\)

So,the polygon has 18 sides

\(75+12+43+25+88+50+57\)

\(=\left(75+25\right)+\left(12+88\right)+\left(43+57\right)+50\)

\(=100+100+100+50=350\)

\(75+12+43+25+88+50+57\)

\(=\left(75+25\right)+\left(12+88\right)+\left(43+57\right)+50\)

\(=100+100+100+50\)

\(=300+50=350\)

75 + 12 + 43 + 25 + 88 + 50 + 57

= ( 75 + 25 ) + ( 43 + 57 ) + ( 12 + 88 ) + 50

= 100 + 100 + 100 + 50

= 300 + 50

= 350