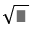In the song "Golden Love", the author of "Do not separate each other" do what?

Answer: Make ashes

$=\frac{\frac{17}{6}+\frac{4}{9}}{\frac{121}{12}-\frac{19}{2}}$

$=\frac{\frac{51}{18}+\frac{8}{18}}{\frac{121}{12}-\frac{114}{12}}$

$=\frac{\frac{59}{8}}{\frac{7}{12}}$

$=\frac{59.12}{7.8}=\frac{177}{14}$

Ans : $B=\frac{177}{14}$.

\(D=-\dfrac{1}{7}\left(9\dfrac{1}{2}-9,75\right):\dfrac{2}{7}+0,625:1\dfrac{2}{3}\)

\(=\left(-1\right).\dfrac{1}{7}:\dfrac{2}{7}.\left(9,5-9,75\right)+\dfrac{5}{8}:\dfrac{5}{3}\)

\(=-\dfrac{1}{2}.\left(-0,25\right)+\dfrac{3}{8}\)

\(=\dfrac{1}{2}+\dfrac{3}{8}=\dfrac{4+3}{8}=\dfrac{7}{8}\)

\(C=1\dfrac{5}{18}:\dfrac{5}{18}\left(\dfrac{1}{15}+1\dfrac{1}{12}\right)\)

\(=\dfrac{23}{18}:\dfrac{5}{18}:\left(\dfrac{1}{15}+\dfrac{13}{12}\right)\)

\(=\dfrac{23}{5}:\dfrac{23}{20}=\dfrac{20}{5}=4\)

The edge of the square is : \(\sqrt{9}=3\) (cm)

Hence,the diagonal OH of the square or the radius of the semicircle is \(3\sqrt{2}\)cm.

The area of the semicircle is : \(\dfrac{\left(3\sqrt{2}\right)^2\pi}{2}=9\pi\)(cm²)

Summer Clouds

 The edge of the square is : 

$\sqrt{9}=3$$\sqrt{\mathrm{<i>9</i>}}<i>=</i>\mathrm{<i>3</i>}$ (cm)

Hence,the diagonal OH of the square or the radius of the semicircle is $3\sqrt{2}$$\mathrm{<i>3</i>}\sqrt{\mathrm{<i>2</i>}}$cm.

The area of the semicircle is : $\frac{{\left(3\sqrt{2}\right)}^2\pi }{2}=9\pi$${\displaystyle \frac{{<i>(</i>\mathrm{<i>3</i>}\sqrt{\mathrm{<i>2</i>}}<i>)</i>}^{\mathrm{<i>2</i>}}\mathrm{<i>\pi </i>}}{\mathrm{<i>2</i>}}}<i>=</i>\mathrm{<i>9</i>}\mathrm{<i>\pi </i>}$(cm2)

x + y = 1 <=> y = 1 - x

We have: F = x² + (1 - x)² + (1 - x).x

                   = x² + 1 + x² - 2x + x - x²

                   = x² - x + 1

                   \(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)

Equal signs occur when and only of \(x-\dfrac{1}{2}=0\) \(\Leftrightarrow x=\dfrac{1}{2}\)

\(y=1-\dfrac{1}{2}=\dfrac{1}{2}\)

min A \(=\dfrac{1}{2}\Leftrightarrow x=y=\dfrac{1}{2}\)

x+y=1             \(\Rightarrow\)\(x^2+2xy+y^2=1\)\(\left(1\right)\)

which \(\left(x-y\right)^2\ge0\)     else \(x^2-2xy+y^2\ge0\left(2\right)\)

plus 1 and 2 we have   \(2\left(x^2+y^2\right)\ge1\Rightarrow x^2+y^2\ge\dfrac{1}{2}\)

minA=\(\dfrac{1}{2}\)      When and only when  x = y = \(\dfrac{1}{2}\)

Because the y value double the x value so : \(y=2x\)

So the function is equal \(2x=3x+6\)

We get x = -6.

So we get y = \(2\cdot\left(-6\right)=-12\)

At the point \(\left(-6;-12\right)\)the y-value double the x-value.

Let  \(\left(x_0;2x_0\right)\) be the coordinates of the point. Since the point belongs to the graph of the function y = 3x + 6,we have :

\(2x_0=3x_0+6\Leftrightarrow x_0=-6\Leftrightarrow2x_0=-12\)

So,the satisfied point is (-6 ; -12)

Apply Cauchy inequality , we have :

\(P=2x+y+\dfrac{30}{x}+\dfrac{5}{y}=\dfrac{4}{5}\left(x+y\right)+\left(\dfrac{6x}{5}+\dfrac{30}{x}\right)+\left(\dfrac{y}{5}+\dfrac{5}{y}\right)\)

\(P\ge\dfrac{4}{5}.10+2.\sqrt{\dfrac{6x}{5}.\dfrac{30}{x}}+2.\sqrt{\dfrac{y}{5}.\dfrac{5}{y}}=8+6+2=16\)

So \(Min_P=16\)

<=> x = y = 5

That is my question ok : https://e-learning.codienhanoi.edu.vn/questions/1902.html

Searching before asking , ok cheater :V

P=4/5(x+y)+(6/5x+30/x)+(y/5+5/y)≥45.10+2√6/5x.30/x+2√y/5.5/y

=8+12+2=22=8+12+2=22

minP=22⇔x=y=5⇔x=y=5

\(x^2+2x+3\)

\(=x^2+2x+1+2\)

\(=\left(x+1\right)^2+2\)

We have:

\(\left(x+1\right)^2⋮x+1\)

\(\Rightarrow2⋮x+1\)

\(\Rightarrow x+1\in\left\{\pm1;\pm2\right\}\)

\(\Rightarrow x\in\left\{-2;0;-3;1\right\}\)

So when x = -2; x = 0; x = -3 or x = 1 

=> \(x^2+2x+3⋮x+1\)

The word "Prove that" is wrong

Let p, n, d, q be the number of pennies, nickels, dimes, quarters we need to make 67 cents respectively (), then p + 5n + 10d + 25q = 67

The answer is 13

Let p, n, d, q be the number of pennies, nickels, dimes, quarters we need to make 67 cents respectively (\(p,n,d,q\in Z^+\)), then p + 5n + 10d + 25q = 67

We have :

(q ; d ; n ; p) = (2 ; 1 ; 1 ; 2) ; (1 ; 3 ; 2 ; 2) ; (1 ; 3 ; 1 ; 7) ; 

(1 ; 2 ; 4 ; 2) ; (1 ; 2 ; 3 ; 7) ; (1 ; 2 ; 2 ; 12) ; (1 ; 2 ; 1 ; 17)

(1 ; 1 ; 6 ; 2) ; (1 ; 1 ; 5 ; 7) ; (1 ; 1 ; 4 ; 12) ; (1 ; 1 ; 3 ; 17) ;

(1 ; 1 ; 2 ; 22) ; (1 ; 1 ; 1 ; 27)

So, the answer is 13