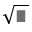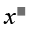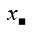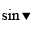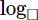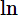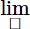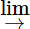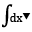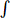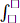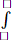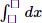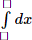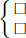-
Cristiano Ronaldo 03/08/2018 at 14:02
Do you want a cookie???
Do you want a nick???
Answer: No, i don't
No , I don't
Hello selected this answer.
-
Fujitora Ishito (online math) ( in the name of love ) 22/03/2017 at 20:09
If p = 2 then p + 8 isn't a prime number.
If p = 3 then p + 8 and p + 16 are prime numbers.
⇒32+(3+8)2+(3+16)2=491⇒32+(3+8)2+(3+16)2=491
If p > 3 then [p=3k+1p=3k+2[p=3k+1p=3k+2
+ If p = 3k + 1 then p + 8 = 3k + 9=3(k+1) isn't a prime number.
+ If p = 3k + 2 then p + 16 = 3k + 18=3(k+6) isn't a prime number.
Answer: 491
Good ^^
-
Trịnh Đức Phát 22/03/2017 at 12:44
If p = 2 then p + 8 isn't a prime number.
If p = 3 then p + 8 and p + 16 are prime numbers.
⇒32+(3+8)2+(3+16)2=491⇒32+(3+8)2+(3+16)2=491
If p > 3 then [p=3k+1p=3k+2[p=3k+1p=3k+2
+ If p = 3k + 1 then p + 8 = 3k + 9=3(k+1) isn't a prime number.
+ If p = 3k + 2 then p + 16 = 3k + 18=3(k+6) isn't a prime number.
Ans: 491.
-
Run my EDM 21/03/2017 at 21:06
If p = 2 then p + 8 isn't a prime number.
If p = 3 then p + 8 and p + 16 are prime numbers.
\(\Rightarrow3^2+\left(3+8\right)^2+\left(3+16\right)^2=491\)
If p > 3 then \(\left[{}\begin{matrix}p=3k+1\\p=3k+2\end{matrix}\right.\)
+ If p = 3k + 1 then p + 8 = 3k + 9=3(k+1) isn't a prime number.
+ If p = 3k + 2 then p + 16 = 3k + 18=3(k+6) isn't a prime number.
Ans: 491.
-
Nguyễn Hiển 14/05/2017 at 22:42FancyKnight#1Jun 27, 2013
As a sequel to the "How many squares on a chessboard" thread, a much more interesting question is the number of possible rectangles on a chessboard, or rather, the method to arrive at this number. This includes squares as well.
The best way I can think of is to seperate these rectangles into three groups:
a) 1x1 squares
b) 1xN rectangles, 1<N<=8
c) Nx1 rectangles, this should be the exact same number as in b)
d) MxN rectangles, 1<N,M<=8
The reason for this split is that i thought of a nice way to get group d):
I believe that every d) rectangle is uniquely defined by a pair of opposite corner squares.
The amount of possible such pairs is 64*49/2=1568,
with the reasoning of picking the first square, and then having 49 squares left to pick which are not on the same rank/file.
Lastly, each rectangle in d) has two possible diagonal pairs which uniquely define it.
Therefore, we have 1568/2=784 rectangles in group
-
Lương Trí Dũng 17/05/2017 at 19:32
784 rectangle in group
-
The sum of the marks is : 17 + 13 + 5 + 10 + 14 + 9 + 12 + 16 = 96
The average of the marks is : 96 : 8 = 12
After removing 2 marks without changing the average,the sum of the marks is : 12 x (8 - 2) = 72
This sum decreased by : 96 - 72 = 24
In the given choices,there's only 10 + 14 = 24.Hence,the answer is E
Selected by MathYouLike -
Trần Nhật Dương 26/06/2017 at 15:35
The sum of the marks is : 17 + 13 + 5 + 10 + 14 + 9 + 12 + 16 = 96
The average of the marks is : 96 : 8 = 12
After removing 2 marks without changing the average,the sum of the marks is : 12 x (8 - 2) = 72
This sum decreased by : 96 - 72 = 24
In the given choices,there's only 10 + 14 = 24.Hence,the answer is E
-
Let a cm be the length of the side,then the length of the corresponding altitude is 2a cm (a > 0).The area of the triangle is :
\(\dfrac{a.2a}{2}=100\Leftrightarrow a^2=100\Leftrightarrow a=10\Leftrightarrow2a=20\)
Hence,the answer is 20 cm or 0,2 m
Selected by MathYouLike
-
AL 07/08/2017 at 17:02
Use AM-GM's inequality we have:
\(\dfrac{abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\le\dfrac{abc}{2\sqrt{ab}\cdot2\sqrt{bc}\cdot2\sqrt{ca}}\)\(=\dfrac{abc}{8abc}=\dfrac{1}{8}\)
Selected by MathYouLike -
Phan Huy Toàn 12/08/2017 at 15:07
AL very good
-
From 10 p.m to 4 a.m. is : (12 - 10) + 4 = 6 (hours)
In 6 hours, the clock gains : 6 x 15 = 90 (minutes) = 1 hour 30 minutes
The clock stopped working at : 4:00 + 1:30 = 5:30 (a.m)
Silas woke up at : 5:30 + 4:00 = 9:30 (a.m)
Selected by MathYouLike -
Sorry. Can I correct 2 last rows ? :
The clock stopped working at : 4:00 - 1:30 = 2:30 (a.m)
Silas woke up at : 2:30 + 4:00 = 6:30 (a.m)
Lê Quốc Trần Anh selected this answer.
-
Nguyễn Tất Đạt 02/09/2017 at 07:56
I have a picture:
From point M, draw ray MN parallel with AC. (N\(\in\)DB)
AB=AD \(\Rightarrow\)\(\Delta\)BAD is an isosceles triangle \(\Rightarrow\widehat{ABD}=\widehat{ADB}\)
But \(\widehat{MNB}=\widehat{ADB}\) (Isotopes)
So \(\widehat{ABD}=\widehat{MNB}\) or \(\widehat{MBN}=\widehat{MNB}\)
\(\Rightarrow\Delta BMN\) is a isosceles triangle \(\Rightarrow BM=MN\).
Because BM=CD \(\Rightarrow MN=CD\).
\(MN\)//AC \(\Rightarrow\)MN//CD \(\Rightarrow\left\{{}\begin{matrix}\widehat{MNI}=\widehat{CDI}\\\widehat{NMI}=\widehat{DCI}\end{matrix}\right.\)
\(\Rightarrow\Delta MIN=\Delta CID\) (Angular angle)
Now we can prove that IM=IC (Corresponding edges)
Phan Thanh Tinh selected this answer.
-
Dao Trong Luan 13/09/2017 at 12:56
A = x2 + 8x + 1
= x2 + 2.x.4 + 16 - 15
= \(\left(x+4\right)^2-15\ge-15\)
=> Minimum of A = -15 at \(\left(x+4\right)^2=0\) and x = -4
B = x2 - x + 1
= \(x^2-2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
=> Minimun of B = \(\dfrac{3}{4}\) at \(\left(x-\dfrac{1}{2}\right)^2=0\) and x = \(\dfrac{1}{2}\)
Selected by MathYouLike