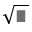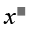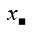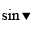-
Help you solve math 20/08/2017 at 20:28
Multiplies of 3,4,5 => Multiplies of 60 (3.4.5)
So the numbers satisfy is: 60,120,180,240,300,360,420,480.60,120,180,240,300,360,420,480.So there are 8 positive integers satisfy the question
Hương Yêu Dấu selected this answer.
-
Luffy xyz 123 20/08/2017 at 20:51
I don't know this question
Because i don't very good at English
Sorry so much.
-
Help you solve math 20/08/2017 at 20:40
Dao Trong Luan was wrong
-
Sherlockkichi 06/08/2018 at 07:07
Do you have evidence against me?
-
Sherlockkichi 07/08/2018 at 00:52
Quoc Tran Anh Le You can not rely on the number of reviews to accuse me of how many nick
-
Nobita - Kun 06/08/2018 at 14:00
?????? what happen in here??
American
09/03/2017 at 09:51
-
An Duong 10/03/2017 at 14:28
The answer id NO.
At the begining there are 32 black pieces. We will prove that the number of black pieces left on the board is always even.
In the single move, we change a row or column, assume that row or column has k black pieces and 8 - k while pieces, after change all black to white and while to black, that row or column will has 8-k black and k white. The difference between black pieces after a single move is (8 - k) - k = 8 - 2k. The difference is a even (8 - 2k). Therefore, after every move, the black pieces left is alaways even and cannot be one black piece at any time.
-
Faded 22/01/2018 at 12:17
The answer id NO.
At the begining there are 32 black pieces. We will prove that the number of black pieces left on the board is always even.
In the single move, we change a row or column, assume that row or column has k black pieces and 8 - k while pieces, after change all black to white and while to black, that row or column will has 8-k black and k white. The difference between black pieces after a single move is (8 - k) - k = 8 - 2k. The difference is a even (8 - 2k). Therefore, after every move, the black pieces left is alaways even and cannot be one black piece at any time.
-
Vũ Việt Vương 01/04/2017 at 16:57
My answer is no.
At the begining there are 32 black pieces. We will prove that the number of black pieces left on the board is always even.
In the single move, we change a row or column, assume that row or column has k black pieces and 8 - k while pieces, after change all black to white and while to black, that row or column will has 8-k black and k white. The difference between black pieces after a single move is (8 - k) - k = 8 - 2k. The difference is a even (8 - 2k). Therefore, after every move, the black pieces left is alaways even and cannot be one black piece at any time.
-
-
I LOVE TFBOYS 25/04/2017 at 20:47
Mỗi người sẽ được 2 quả ( nếu được chia đều cho nhau)
-
hot girl cua lop 25/04/2017 at 20:46
two oranges
falcon handsome moderators
09/03/2017 at 12:27
-
Ace Legona 09/03/2017 at 19:22
Let \(S\) be the sum of all the \(mn\) numbers in the table. Note that after an operation, each number stay the same or turns to its negative. Hence there are at most \(2^{mn}\) tables. So \(S\) can only have finitely many possible values. To make the sum of the numbers in each line nonnegative, just look for a line whose numbers have a negative sum. If no such line exists, then we are done. Otherwise, reverse the sign of all the numbers in the line. Then \(S\) increases. Since \(S\) has finitely many possible values, \(S\) can increase finitely many times. So eventually the sum of the numbers in every line must be nonnegative.
-
FA FIFA Club World Cup 2018 16/01/2018 at 21:57
Let SS be the sum of all the mnmn numbers in the table. Note that after an operation, each number stay the same or turns to its negative. Hence there are at most 2mn2mn tables. So SS can only have finitely many possible values. To make the sum of the numbers in each line nonnegative, just look for a line whose numbers have a negative sum. If no such line exists, then we are done. Otherwise, reverse the sign of all the numbers in the line. Then SS increases. Since SS has finitely many possible values, SS can increase finitely many times. So eventually the sum of the numbers in every line must be nonnegative
-
Nguyễn Anh Tuấn 24/03/2017 at 17:49
Let SS be the sum of all the mnmn numbers in the table. Note that after an operation, each number stay the same or turns to its negative. Hence there are at most 2mn2mn tables. So SS can only have finitely many possible values. To make the sum of the numbers in each line nonnegative, just look for a line whose numbers have a negative sum. If no such line exists, then we are done. Otherwise, reverse the sign of all the numbers in the line. Then SS increases. Since SS has finitely many possible values, SS can increase finitely many times. So eventually the sum of the numbers in every line must be nonnegative.
-
-
Thanh Trà 13/08/2017 at 20:05
x + \(\dfrac{2}{5}\) = \(\dfrac{1}{2}\)
x = \(\dfrac{1}{2}\) + \(\dfrac{2}{5}\)
x = \(\dfrac{9}{10}\)
-
-
Give A = 22 + 24 + .... + 2100
4A = 24 + .... + 2100 + 2102
4A - A = (24 + .... + 2100 + 2102) - (22 + 24 + .... + 2100)
3A = 2102 - 22
A = \(\dfrac{2^{102}-4}{3}\)
Asuna Yuuki selected this answer. -
Vũ Thị Hương Giang 09/03/2017 at 21:47
Ta có : A = 22 + 24 + 26 + ...... + 2100
=> 22A = 24 + 26 + ...... + 2100 + 2102
=> 4A - A = 2102 - 22
=> 3A = 2102 - 4
=> A = \(\dfrac{2^{102}-4}{3}\)
-
demo acc 10/03/2017 at 14:44
very good


-
FA FIFA Club World Cup 2018 16/01/2018 at 22:03
ab=a(b+c)b(b+c)=ab+acb2+bc
a+cb+c=b(a+c)b(b+c)=ab+bcb2+bc
In here , we have :
b2 + bc = b2 + bc
ab = ab
If a>b
=> ac > bc (when a,b ∈N
)
=> ab>a+cb+c
If a<b
=> ac < bc (when a,b ∈N
)
=> ab<a+cb+c
-
Asuna Yuuki 09/03/2017 at 21:55
We can see :
If \(\dfrac{a}{b}< 1\)=> a < b
=> ac < ab
=> a. ( b + c ) < b. ( c + a )
=> \(\dfrac{a}{b}< \dfrac{a+c}{b+c}\)
-
\(\dfrac{a}{b}=\dfrac{a\left(b+c\right)}{b\left(b+c\right)}=\dfrac{ab+ac}{b^2+bc}\)
\(\dfrac{a+c}{b+c}=\dfrac{b\left(a+c\right)}{b\left(b+c\right)}=\dfrac{ab+bc}{b^2+bc}\)
In here , we have :
b2 + bc = b2 + bc
ab = ab
If a>b
=> ac > bc (when a,b \(\in N\))
=> \(\dfrac{a}{b}>\dfrac{a+c}{b+c}\)
If a<b
=> ac < bc (when a,b \(\in N\))
=> \(\dfrac{a}{b}< \dfrac{a+c}{b+c}\)
-
Every positive integer has a unique representation in base 2. This is the same as saying that each positive integer can be written uniquely as a sum of different powers of 2. For example, 1 = 20 ,2 = 21 ,3 = 20 + 22 , and so on. Recall that we are interested in the numbers beginning x1 = 30 , x2 = 31 , and x3 = 30 + 31 . We can find the nth term in this sequence by writing n as a sum of different powers of 2 and then replacing each 2j in the sum by 3j . Since n = 100 can be written in base 2 as n = (1100100)2, we get 100 = 22 + 25 + 26 so that x100 = 32 + 35 + 36 = 9 + 243 + 729 = 981
Carter selected this answer. -
tin123tin 27/04/2017 at 15:28
x100 = x98 + x99 = 3^97 + 3^98 = 3.(3^96+3^97)