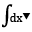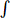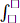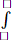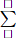We have :

\(\widehat{A}=3\widehat{B}\) => \(\widehat{B}=\dfrac{\widehat{A}}{3}\)  (1)

\(2\widehat{A}=\widehat{C}\)  (2)

Apply a total of 3 corners in a triangle :

\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

Change (1) and (2) in this equality :

=> \(\widehat{A}+\dfrac{\widehat{A}}{3}+2\widehat{A}=180^0\)

=> \(\dfrac{10}{3}\widehat{A}=180^0\)

=> \(\widehat{A}=54^0\)

According to the problem, we have:

\(\widehat{A} = 3 \widehat{B}\)\(\Rightarrow\)\(\widehat{B}=\frac{\widehat{A}}{3}\)  (1)

\(\widehat{C}=2\widehat{A}\) (2)

\(\widehat{A} + \widehat{B} + \widehat{C}=180^0\) (3)

Change (1)(2) to (3) we have:

\(\widehat{A} + \frac{\widehat{A}}{3}+2\widehat{A}=180^0\)

\(\frac{10}{3}\widehat{A}=180^0\)

\(\widehat{A} = 54^0\)

\(\Rightarrow\) (C) is correct

Denote A = n²(n⁴ - 1) = n²(n² - 1)(n² + 1) is the product of 3 consecutive integers,so \(A⋮3\).We have :

\(\circledast A=n^2\left(n-1\right)\left(n+1\right)\left(n^2+1\right)\)

If n is even,then \(n^2⋮4\) and \(A⋮4\)

If n is odd,then n - 1 and n + 1 is even. So,\(A⋮4\)

Hence,\(A⋮4\)

\(\circledast A=n^2\left(n^2-1\right)\left(n^2-4\right)+5n^2\left(n^2-1\right)\)

\(=\left(n-2\right)\left(n-1\right)n^2\left(n+1\right)\left(n+2\right)+5n^2\left(n^2-1\right)\)

\(\left(n-2\right)\left(n-1\right)n^2\left(n+1\right)\left(n+2\right)\)include the product of 5 consecutive integers,so it's divisible by 5.Moreover, \(5n^2\left(n^2-1\right)⋮5\)

Hence,\(A⋮5\)

Since A is divisible by 3,4,5 and 3,4,5 are relatively prime numbers, \(A⋮3.4.5=60\)

One digit: 9 (numbers)
Two digits: 9 (numbers)
... 9 Digits: 9 (numbers)

So there are : \(9\cdot9=81\) (numbers)

Answer : There are 81 integers less than one billion are very round numbers.

3^{n + 2} - 2^{n + 2} + 3ⁿ - 2ⁿ

= 3ⁿ.9 + 3ⁿ - 2ⁿ.4 - 2ⁿ

= 3ⁿ.10 - 2ⁿ.5

= 3ⁿ . 10 - 2^{n - 1} . 10

= 10.(3ⁿ - 2^{n - 1})  \(⋮10\forall n\)

3^{n + 2} - 2^{n + 2} + 3ⁿ - 2ⁿ

= 3ⁿ.9 + 3ⁿ - 2ⁿ.4 - 2ⁿ

= 3ⁿ.10 - 2ⁿ.5

= 3ⁿ . 10 - 2^{n - 1} . 10

= 10.(3ⁿ - 2^{n - 1})  

If Phara buy all items, she must cost:

$2.99 + $3.49 + $6.29 + $4.99 + $3.89 + $5.49 = $27.14

So she it took more: $27.14 - $17.36 = $9.78

But $9.78 is the sum money must cost of Puzzle and Wallet.

So she didn't bought Puzzle and Wallet

So the positive difference of their is:

$6.29 - $3.49 = $2.8

So she it took more:  17.36 = 9.78 $

But $9.78 is the sum money must cost of Puzzle and Wallet.

So she didn't bought Puzzle and Wallet

So the positive difference of their is:

3.49 = 2.8$

When the water level rises 1 in, the amount of water in the tank increases by : 10 x 15 x 1 = 150 (in³)

The volume of each sphere is : \(\dfrac{4}{3}\pi\left(\dfrac{1}{6}:2\right)^3=\dfrac{1}{1296}\pi\) (in³)

The answer is : \(150:\dfrac{1}{1296}\pi\approx61900\) (spheres)

5 days

We have: \(\dfrac{\left(4\times7+2\right)\left(6\times9+2\right)...\left(100\times103+2\right)}{\left(5\times8+2\right)\left(7\times10+2\right)...\left(99\times102+2\right)}=\dfrac{5\times6\times7\times8\times...\times101\times102}{6\times7\times8\times9\times...\times100\times101}=5\times102=510\)

Thank you !!!!!!!!! :D