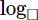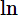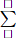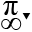\(2^{32}=\left(2^4\right)^8=16^8\) has 6 as the last digit

So the answer is 6

Summer Clouds 

$2^{32}={\left(2^4\right)}^8={16}^8$${\mathrm{<i>2</i>}}^{\mathrm{<i>32</i>}}<i>=</i>{<i>(</i>{\mathrm{<i>2</i>}}^{\mathrm{<i>4</i>}}<i>)</i>}^{\mathrm{<i>8</i>}}<i>=</i>{\mathrm{<i>16</i>}}^{\mathrm{<i>8</i>}}$ has 6 as the last digit

So the answer is 6

6 là ansewr

Sorry, can I answer again?

\(\left(x+2\right)\left|x+3\right|=0\)

=> \(\left(x+2\right)=0\) or \(\left|x+3=0\right|\)

=> \(x=\left\{-2;-3;-6\right\}\)

So the answer is \(x=\left\{-2;-3;-6\right\}\) (Phan Thanh Tinh miss one answer)

\(\left(x+2\right)\left|x+3\right|=0\Rightarrow\left[{}\begin{matrix}x+2=0\\\left|x+3\right|=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\)

So,-2 and -3 are negative roots of the equation above.

In the first month the fund gains 20% so the total fund of him after the first month is :

\(5000\cdot120\%=6000\)$

At the end of second month Arturo loses 20% of its value, so Arturo's investment worth at that time is :

\(6000\cdot80\%=4800\)$

So the answer is 4800$.

We need to press a button in order 3 times at least :

S - H - S - H

H - S - H - H

H - H - S - S

H - H - H - H

The area of the square triangle is:

     \(\dfrac{12.5}{2}=30\)

The area of the semicircle is:

      \(\dfrac{\dfrac{13}{2}.\dfrac{13}{2}.3,14}{2}=\dfrac{26533}{400}=66,3325\)

The total area of the shaded regions is:

       66,3325-30=36,3325\(\approx36\)

Answer:36

The answer is 36

it is correct?

The area of the square triangle is:

     12.52 = 3012 . 52 = 30

The area of the semicircle is:

      132.132.3,142 = 26533400 = 66,3325132.132.3,142 = 26533400 = 66,3325

The total area of the shaded regions is:

       66,3325 - 30 = 36,33253636

Answer:36

M = \(1-\dfrac{1}{2^2}+\dfrac{1}{2^2}-\dfrac{1}{3^2}+...+\dfrac{1}{2015^2}-\dfrac{1}{2016^2}\)

M = \(1-\dfrac{1}{2016^2}=1-\dfrac{1}{4064256}=\dfrac{4064255}{4064256}\)

We have: \(\dfrac{2n+1}{\left(n^2+n\right)^2}=\dfrac{\left(n+1\right)^2-n^2}{n^2\left(n+1\right)^2}=\dfrac{1}{n^2}-\dfrac{1}{\left(n+1\right)^2}\)

So: \(M=\dfrac{2.1+1}{\left(1^2+1\right)^2}+\dfrac{2.2+1}{\left(2^2+2\right)^2}+...+\dfrac{2.2015+1}{\left(2015^2+2015\right)^2}\)

            \(=1-\dfrac{1}{2^2}+\dfrac{1}{2^2}-\dfrac{1}{3^2}+...+\dfrac{1}{2015^2}-\dfrac{1}{2016^2}\)

            \(=1-\dfrac{1}{2016^2}< 1\)

M = 1−122+122−132+...+120152−120162

M = 1−120162=1−14064256=40642554064256