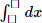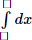a, consider the triangle AHFK: \(\widehat{A}=\widehat{H}=\widehat{K}=90^o\)

should AHFK is rectangle

b,  consider the triangle ACF :OA=OC;EC=EF

should OE is the average line of the triangle ACF

should OE//AF or AF//BD

similar: the average line is EJ triangle ACF 
should EJ//AC

similar: the average line is EJ triangle ACF 
should EJ//AC

\(\Rightarrow\widehat{AKJ}=\widehat{KAJ}+\widehat{KAJ}=\widehat{KDE}\)pairs of isotopes

\(\Rightarrow\widehat{AKJ}=\widehat{KDE}\) or KDE loss triangle

inferred :\(\widehat{JK}=\widehat{DEK}=\dfrac{180-KDE}{2}\) should K; J and E line 
that K; J; H line 
should K; H and E also in line and HK//AC

Sorry, can I fix the answer?

The probability of the die shows a prime number from 1-6 (The numbers: 2;3;5): \(1:2=\dfrac{1}{2}\)

So their probability are: \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}=25\%\)

The probability that the coin lands head up is: \(1:2=\dfrac{1}{2}\)

The probability that the die rolls as a prime number from 1-6 (The numbers are: 4): \(1:6=\dfrac{1}{6}\)

So their probability are: \(\dfrac{1}{2}.\dfrac{1}{6}=\dfrac{1}{12}\)

Let n be the number of edges of the polygon \(\left(n\in N;n>2\right)\)

We have : \(180\left(n-2\right)=1260\Leftrightarrow n-2=7\Leftrightarrow n=9\)

So, the polygon has 9 sides.

Let n be the of edges of the polygon and (n ∈ N, n > 2)

We have :

180 . (n - 2) = 1260 <=> n - 2 = 7 => n = 9

Answer: 9 sides

Let n be the of edges of the polygon and (n ∈ N, n > 2)

We have :

180 . (n - 2) = 1260 <=> n - 2 = 7 => n = 9

Answer: 9 sides
 

The first reflection changes P(-3 ; -2) to (2 ; 3). The answer is :

(2 + 4 ; 3 - 1) = (6 ; 2)

The first reflection changes  P(-3; -2) to (2; 3)

The answer is: 

(2 + 4; 3 - 1) = (6; 2)

Let a, b be the price of an oldies CD and a current CD respectively.

We have :

(2a + 3b) - (3a + 2b) = 82 - 78 <=> b - a = 4

So, the answer is 4

Let a, a + 1, a + 2, ... , a + 10 be the integers. We have :

\(a+\left(a+1\right)+\left(a+2\right)+...+\left(a+10\right)=11\)

\(\Leftrightarrow11a+\dfrac{10.11}{2}=11\Leftrightarrow a+\dfrac{10}{2}=1\Leftrightarrow a=-4\)

So, the answer is -4

4 > 3 => 45777 > 35777

And 35777 > 35674

==> 45777 > 35674

P/s Mk chỉ biết 4⁵⁷⁷⁷ > 3⁵⁶⁷⁴ vì dễ thấy mà mk cũng không biết cách trả lời

Bạn là người copy câu trả lời của Đào Trọng luân

\(Q=\dfrac{3\left(x+1\right)}{x^3+x^2+x+1}=\dfrac{3\left(x+1\right)}{\left(x+1\right)\left(x^2+1\right)}=\dfrac{3}{x^2+1}\)

We have: \(x^2\ge0\forall x\Leftrightarrow x^2+1\ge1\forall x\)

\(\Leftrightarrow\dfrac{1}{x^2+1}\le1\forall x\)

\(\Leftrightarrow Q=\dfrac{3}{x^2+1}\le3\forall x\)

\("="\Leftrightarrow x=0\)