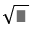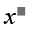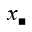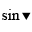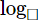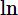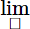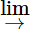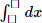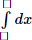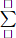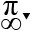It Thai Son mountain.

Núi Thái Sơn nha Bạn

Sorry: What the mountains cut into pieces?

For any natural number n > 1,we have :

(n - 1)n(n + 1) = n(n2 - 1) = n3 - n < n3

⇒1n3<1(n−1)n(n+1)

1(n−1)n(n+1)=1n.1(n−1)(n+1)

=1n.(n+1)−(n−1)(n−1)(n+1).12=12.1n.(1n−1−1n+1)

=12.(1(n−1)n−1n(n+1))

Now we have :

E < 12.3.4+13.4.5+14.5.6+...+1(n−1)n(n+1)

=12(12.3−13.4)+12(13.4−14.5)+12(14.5−15.6)+...+12(1(n−1)n−1n(n+1))

=12(12.3−1n(n+1))=112−12n(n+1)<112

Hence,E<112

For any natural number n > 1,we have :

(n - 1)n(n + 1) = n(n² - 1) = n³ - n < n³

\(\Rightarrow\dfrac{1}{n^3}< \dfrac{1}{\left(n-1\right)n\left(n+1\right)}\)

\(\dfrac{1}{\left(n-1\right)n\left(n+1\right)}=\dfrac{1}{n}.\dfrac{1}{\left(n-1\right)\left(n+1\right)}\)

\(=\dfrac{1}{n}.\dfrac{\left(n+1\right)-\left(n-1\right)}{\left(n-1\right)\left(n+1\right)}.\dfrac{1}{2}=\dfrac{1}{2}.\dfrac{1}{n}.\left(\dfrac{1}{n-1}-\dfrac{1}{n+1}\right)\)

\(=\dfrac{1}{2}.\left(\dfrac{1}{\left(n-1\right)n}-\dfrac{1}{n\left(n+1\right)}\right)\)

Now we have :

E < \(\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+\dfrac{1}{4.5.6}+...+\dfrac{1}{\left(n-1\right)n\left(n+1\right)}\)

\(=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)+\dfrac{1}{2}\left(\dfrac{1}{3.4}-\dfrac{1}{4.5}\right)+\dfrac{1}{2}\left(\dfrac{1}{4.5}-\dfrac{1}{5.6}\right)+...+\dfrac{1}{2}\left(\dfrac{1}{\left(n-1\right)n}-\dfrac{1}{n\left(n+1\right)}\right)\)

\(=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{n\left(n+1\right)}\right)=\dfrac{1}{12}-\dfrac{1}{2n\left(n+1\right)}< \dfrac{1}{12}\)

Hence,\(E< \dfrac{1}{12}\)

We have :

\(=\dfrac{\left(x^3+x^2\right)-\left(x+1\right)}{x^2-5x-x+5}\)

\(=\dfrac{x^2\left(x+1\right)-\left(x+1\right)}{x\left(x-1\right)-5\left(x-1\right)}\)

\(=\dfrac{\left(x-1\right)\left(x+1\right)^2}{\left(x-5\right)\left(x-1\right)}\)

\(=\dfrac{\left(x+1\right)^2}{x-5}\)
 

The first such triple is 8 = \(2^2+2^2\),9 = \(3^3+0^2\),10=\(3^2+1^2\), which suggests we consider triples \(x^2-1,x^2,x^2+1\).Since \(x^2-2y^2=1\) has infinitely many positive solutions (x,y), we see that \(x^2-1=y^2+y^2,x^2=x^2+0^2\)and \(x^2+1\) satisfy the requiment and there are infinitely many such triples.

The first such triple is 8 = 22+22,9 = 33+02,10=32+12, which suggests we consider triples x2−1,x2,x2+1.Since x2−2y2=1 has infinitely many positive solutions (x,y), we see that x2−1=y2+y2,x2=x2+02and x2+1 satisfy the requiment and there are infinitely many such triples.

Wowe it hard

a.

\(x^2-2y^2=xy\)

\(\Leftrightarrow x^2-2y^2-xy=0\)

\(\Leftrightarrow\left(x^2-y^2\right)-\left(y^2+xy\right)=0\)

\(\Leftrightarrow\left(x-y\right)\left(x+y\right)-y\left(x+y\right)=0\)

\(\Leftrightarrow\left(x+y\right)\left(x-y-y\right)=0\)

\(\Leftrightarrow\left(x+y\right)\left(x-2y\right)=0\)

But \(x+y\ne0\)

\(\Rightarrow x-2y=0\Leftrightarrow x=2y\)

\(\Rightarrow P=\dfrac{x-y}{x+y}=\dfrac{2y-y}{2y+y}=\dfrac{y}{3y}=\dfrac{1}{3}\)

Continue Dao Trong Luan'answer:

\(\left(x-1\right)\left[x^2-4\left(x-1\right)\right]\)

\(=\left(x-1\right)\left(x^2-4x+4\right)\)

\(=\left(x-1\right)\left(x-2\right)^2\)

I edited the subject

We have :

(x - 1) . [x² - 4 . (x - 1)]

<=> (x - 1) . (x² - 4x + 4)

=> (x - 1). (x - 2)²

This is brief

We have:\(\left(x+1\right)\left(x-3\right)-\left(x+5\right)\left(x-5\right)\left(x-2\right)=0\)

\(\Leftrightarrow x^2-2x-3-\left(x^2-25\right)\left(x-2\right)=0\)

\(\Leftrightarrow x^2-2x-3-x^3+2x^2+25x-50=0\)

\(\Leftrightarrow3x^2-x^3+23x-53=0\)

\(\Leftrightarrow x^2\left(3-x\right)-23\left(3-x\right)+16=0\)

\(\Leftrightarrow\left(x^2-23\right)\left(3-x\right)+16=0\)

\(\Rightarrow x^2-23\in\left\{-16,-8,-4,-2,-1,1,2,4,8,16\right\}\)

\(\Rightarrow x^2\in\left\{7,15,19,21,22,24,25,27,31,39\right\}\)

Because 3-x is a integer number so x is a integer number so \(x^2=25\) and 3-x=-8

\(\Rightarrow\) x=\(\pm\)5 and x=11 (unsatisfactory)

So not have x satisfy

Stop Touching YourSelf, please =((

Put the equation above is \(\left(1\right)\)

If \(xy>0\) then:

\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\dfrac{17}{y}+\dfrac{2}{x}=2011\\\dfrac{1}{y}-\dfrac{2}{x}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1007}{9}\\\dfrac{1}{x}=\dfrac{490}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{9}{490}\\y=\dfrac{9}{1007}\end{matrix}\right.\) (satisfy)

If  \(xy< 0\) then:

\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\dfrac{17}{y}+\dfrac{2}{x}=-2011\\\dfrac{1}{y}-\dfrac{2}{x}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=-\dfrac{1004}{9}\\\dfrac{1}{x}=-\dfrac{1031}{18}\end{matrix}\right.\)\(\Rightarrow xy>0\)  (unsatisfactory)

If \(xy=0\) then: \(\left(1\right)\Leftrightarrow x=y=0\) (satisfy)

Conclude: equations have 2 solutions: \(\left(0;0\right)\) and \(\left(\dfrac{9}{490};\dfrac{9}{1007}\right)\)

\(2\left(x^2+\dfrac{1}{x^2}\right)+3\left(x+\dfrac{1}{x}\right)-16=0\left(1\right)\)

Condition: \(x\ne0\)

Put \(t=x+\dfrac{1}{x}\Rightarrow x^2+\dfrac{1}{x^2}=t^2-2\)

\(\left(1\right)\Leftrightarrow2t^2+3t-20=0\) \(\Leftrightarrow\left[{}\begin{matrix}t=-4\\t=\dfrac{5}{2}\end{matrix}\right.\)

If \(t=-4\Rightarrow x=-2\pm\sqrt{3}\)

If \(t=\dfrac{5}{2}\) \(\Rightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{2}\end{matrix}\right.\)

Conclude:...